(중요!!!!)
미분방정식을 설명하기 위해서, 다음과 같은 논리를 적용할 것이다.
1. 일단 해를 어떻게든 구한다!!! (즉, 어떤 논리를 통해서 해를 구했다... 라기보다는, 일단 이런 식의 방법으로 해를 구할 수 있다는 것을 보인다.)
2. 구한 해가 "유일하다"는 것을 보인다!
즉, 뒷 챕터에서 나올 Integrating Factor나 변수분리법 등에서 이러이러해서 이렇게 해를 구했다! 라기 보다는(즉, 논리가 있기 보단)
일단, 어떻게 가정하면 해를 구할 수 있고 -> 이렇게 구한 해가 유일하다!
라는 식의 논리로 진행을 한다!
이런 식으로 설명을 하는 이유는 비선형 미분방정식의 해를 구하는 방법 자체가 따로 정해져 있지 않기 때문이다.
(물론, 선형인 경우에는 Formal한 방식을 적용할 수 있다.)
이 논리는 뒤에서 나올 Integrating Factor와 변수분리법에서 볼 수 있으므로 참고!!
이번 챕터에서는 1st-order ODE를 어떻게 푸는지 볼 것이다. 푸는 방법을 알아두면 고등학교 시험같은데에서도 충분히 쓸수 있으니, 알아두면 좋다.
(NOTE)
조건이 아무것도 없고, 그냥 미분방정식 식만 있다면
일반적으로 미분방정식의 해는 "하나"가 아니다!!!
(조건이 더해지면 해가 정해진다. -> 적분상수를 "초기조건"을 통해서 결정하는 것을 생각하면 된다!)
1. Linear Case
선형미분방정식의 경우 일반적으로 다음과 같이 쓸 수 있다.
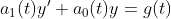
이 때, a1(t)는 모든 t에서 0이 되지 않는다. (0이 되면, 1차미분방정식이 아님!!)
그러므로 다음과 같이 쓸 수 있다.
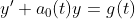
이 미분방정식을 풀어보자!!!
1-1. 각 Coefficient가 t에 대한 함수가 아니라 상수인 경우
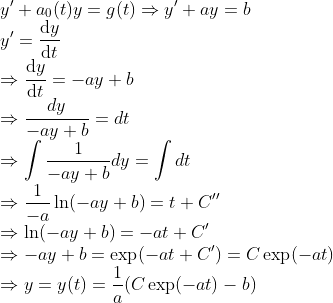
이 때, C는 적분 상수이므로, 조건 하나가 더 들어오면 결정이 되는 상수이다.

=> 이 방법에서의 키 포인트는, y와 t를 분리해서 따로 적분을 하는 것이다!!
=> 이런 식으로 변수를 분리해서 적분을 할 수 있다면, 이 식을 "변수분리가 가능한 식"(Separable Equation)이라고 한다.
그러나, 일반적인 경우
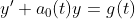
변수 분리가 깔끔하게 되지 않는 것을 볼 수 있다...
그러면, 이 Separable Equation인지 알 수 있는 방법이 있을까???
다시 일반화된 식을 본다면....
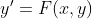
일 텐데, 여기서

즉, 분자는 t에 관한 식, 분모는 y에 관한 식으로 쪼개어진다면, 굳이 선형방정식이 아니어도 -> 문제를 풀 수 있다!!!
즉, 이런 식으로 변수를 분리해서 적분을 할 수 있다면, 심지어 "비선형"인 경우에도 문제를 풀 수 있을 것이다.
ex1)

ex2)

즉, Closed-form으로는 나오지 않지만, 저 식을 만족하는 y가 위 미분방정식의 해가 된다. (물론, 해가 유일하지는 않을 수 있다.)
1-2. a_0만 상수인 경우
이 경우에는 두가지 방법으로 생각해본다.
1-2-1. "Non-homogeneous 선형" 미분방정식에 적용이 되는 방식
챕터 1. Classification of Differential Equation에서 언급된 방법으로, Homogeneous Solution과 Special Solution으로 나누어 생각해보자.
먼저, 각 용어에 대해서 정리해보자.
(a) Homogeneous Solution -> g(t)=0인 경우의 solution
즉, 다음과 같이 생각하면 된다.

우리의 예시를 적용해보면

일반적으로 선형인 경우(굳이 1차가 아니어도) Homogeneous solution은 쉽게 구할 수 있다.
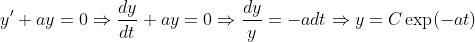
C는 적분상수이므로, 조건이 하나 더 들어와야지 결정이 된다. -> 즉, Homogeneous Solution은 조건이 없다면 아직 결정되지 않았다!!!
(b) Special Solution(특수해) -> 주어진 g(t)에 대해서 그냥 solution 하나 잡기!

예를 들어서...
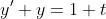
의 특수해는 그냥 y_p=t라고 할 수 있다.
왜냐하면,

이 때, 특수해는 Homogeneous solution과는 다르게 적분상수가 없으므로 딱 결정되어 있다!(물론, 특수해가 유일하다는 것은 아니다. 특수해가 여러개 있을 수도 있지만, 우리는 그 중 그냥 하나만 잡는다.)
(c) General Solution(일반해)
일반해는 Homogeneous Solution과 Special Solution의 합으로 쓸 수 있다. 왜냐하면

이 경우도 조건이 아무것도 안 달려있기 때문에 여러 개의 해가 나올 수 있는데, 이는 Homogeneous solution의 적분상수가 아직 안 정해졌기 때문으로 보면 된다!!
(NOTE)
특수해를 다른 것으로 잡아도, 나중에 조건을 적용해서 해를 고정시킬 때, 적분상수가 달라지면서 결국 똑같은 해가 나오게 된다.
결론적으로

의 해는 다음과 같이 쓸 수 있다.
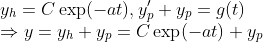
그런데, 저 특수해는 g(t)를 알아야지 구할 수 있고, g(t)의 모양이 복잡해지면 구하기도 어려워진다....
(특수해를 구하는 방법은 나중에 설명하겠지만, 위의 예시처럼 g(t)의 모양이 어느 정도 정해져야 구할 수 있다.)
그러나, Non-homogeneous Form에서 가장 일반적으로 쓰이는 방법이므로 꼭 알아두자!!!
다음에 나올 Integrating Factor와 변수분리방법은 다음 글에서 설명한다!
'Mathematics > 미분방정식' 카테고리의 다른 글
| (미분방정식) 3-2. Existence & Uniqueness of solution of 1st-ODE (2) (1) | 2023.11.12 |
|---|---|
| (미분방정식) 3-1. Existence & Uniqueness of solution of 1st-ODE (1) (0) | 2023.11.11 |
| (미분방정식) 2-2. 1st-Order ODE (2) (0) | 2023.11.05 |
| (미분방정식) 1. Classification of Differential Equation (0) | 2023.11.05 |
| (미분방정식) 미분방정식 개요 (0) | 2023.11.05 |



