먼저 미분방정식 카테고리에서 사용할 용어들을 정리해보도록 한다.
(미분방정식 -> 1변수)
x에 대한 식 y=f(x)에 대해서, 다음 방정식 F의 해 y=f(x)를 구하는 방정식을 말한다.
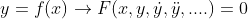
이 때, y는 x에만 관련되어 있는 일변수 함수이므로, y', y'' ... 는 편미분이 아니라 상미분이다. 그러므로 이렇게 생긴 미분방정식을 "상미분방정식(Ordinary Differential Equation; ODE)"이라고 한다.
ex1)

ex2)
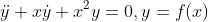
또한, 미분방정식에서 가장 미분을 많이 한 항을 기준으로 n차 미분방정식(nth-order Differential Equation)이라고 한다.
(즉, ex1은 1차(1st-order)미분방정식, ex2는 2차미분방정식)
(미분방정식 -> 다변수)
위와는 다르게 y=f(x_1,x_2,....,x_n)으로 y가 다변수함수인 경우, y를 미분할 때 "편미분"이 튀어나오게 된다.
이렇게 편미분항이 들어간 미분방정식을 "편미분방정식(Partial Differential Equation; PDE)"라고 한다.
ex)
u=u(t,x,y)로 다변수함수인 경우

(Systems of Differential Equation)
연립미분방정식을 말한다.
ex)

(NOTE)
고차선형상미분방정식은 연립미분방정식으로 쓸 수 있다!
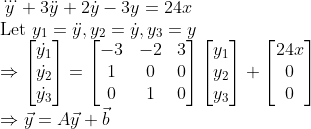
그러므로 결국 고차미분방정식을 => 선형연립미분방정식으로 생각한다!!!
(Linear/Nonlinear Differential Equation)
선형/비선형 미분방정식을 말한다.
ODE에서 선형미분방정식의 꼴은...

즉, 고차선형미분방정식으로 쓴다면

이런 형식으로 미분방정식을 쓸 수 없다면, 비선형 미분방정식이 된다.
ex) 아래처럼 간단한 미분방정식도 일단 비선형이다!
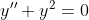
(NOTE1)
사실, 선형대수학을 알고 있다면 다음 표현이 더 명확하다.

즉, 미분방정식 F(x,....)를 y에 대한 함수로 보았을 때, 선형조건을 만족한다면, 이 F는 선형미분방정식이다.
ex1) 선형미분방정식
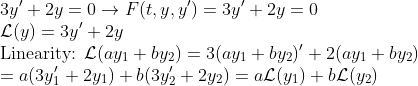
ex2) 비선형미분방정식

(NOTE2)
사실 위에서

g(x)가 0이 아니면, (NOTE1)에서 본 선형성을 만족하지 않는다.
그러나 나중에 이 문제는
1. Homogeneous Solution(g(x)=0인 경우의 해),
2. Special Solution (g(x)가 들어갔을 때 해를 하나 그냥 잡는다!)
으로 나누어서 문제를 푼 후,
=> (일반해) = (Homogeneous Solution) + (Special Solution)가 되므로
결국 선형 문제를 푸는 것과 동일해진다. 그러므로, 여기서는 선형으로 생각한다.
(이러한 Form을 Non-homogeneous form이라고도 한다.)
또한, 위에서 g(x)=0인 경우를 "Homogeneous Form"이라고도 한다!
'Mathematics > 미분방정식' 카테고리의 다른 글
| (미분방정식) 3-2. Existence & Uniqueness of solution of 1st-ODE (2) (1) | 2023.11.12 |
|---|---|
| (미분방정식) 3-1. Existence & Uniqueness of solution of 1st-ODE (1) (0) | 2023.11.11 |
| (미분방정식) 2-2. 1st-Order ODE (2) (0) | 2023.11.05 |
| (미분방정식) 2-1. 1st-Order ODE (1) (0) | 2023.11.05 |
| (미분방정식) 미분방정식 개요 (0) | 2023.11.05 |



