(참고링크)
(선형대수학) 7-1. Inner Product(내적)과 Norm : https://0418cshyun.tistory.com/157
(선형대수학) 7-1. Inner Product(내적)과 Norm
이번 챕터에서는 이미 쉽게 알고 있을 벡터의 내적(Inner Product)과 Norm에 대해서 살펴보자. 먼저, 벡터의 내적(Inner Product)에 대해서 정의하자. 대부분 이 글을 보는 사람들은 이미 내적에 대해서 알
0418cshyun.tistory.com
위의 링크에서 "복소수" 벡터의 Inner Product, Norm에 대해서 살펴보고 오자!!
먼저, 챕터 11에서 했던 Diagonalization에 대한 내용은 실수 행렬인 경우에 국한된다고 말했었다!
그러면, 이를 복소수 행렬(Complex Matrix)로 확장시키면 어떻게 변하길래 따로 챕터를 뽑아놓았을까...?
Diagonalization을 하기 위해서 Eigenvalue Problem을 푸는 과정을 생각해보자!

Real Matrix(실수 행렬)인 경우, 행렬식이 n차 "실수 계수" 방정식이 되고,
Complex Matrix인 경우, 행렬식이 n차 "복소수 계수" 방정식이 된다.
이게 무슨 의미가 있나 싶지만....
(LEMMA)
n차 "실수 계수" 방정식의 해가 x=a+bi라면, 그 켤레수(conjugate number) x=a-bi 또한 이 방정식의 해이다.
만일, 실수 -> 복소수로 확장한다면, 켤레복소수가 해가 아닐 수도 있다!
(증명)
1. 실수계수인 경우
여러 방법으로 증명할 수 있겠지만, 그냥 식을 다 풀어보자!

(여기서 f,g에서 생략된 부분들은 모두 실수!! (오직 a_i와 p에 대한 식))

그러므로, 켤레복소수도 해가 된다.
2. 복소수계수인 경우
위의 증명과 같은 방식으로 f, g를 유도할 때, a_n이 복소수이므로, 모든 a_i들을 결국에는 실수/허수부로 쪼개야 정확한 f,g가 나온다. 물론 너무 복잡해지므로 그냥 반례를 하나 보고 넘어가도록 하자!
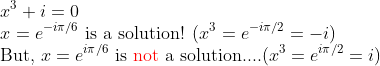
(극좌표계로 생각해보면, 더 쉽게 생각해볼 수 있다...)
그러므로, Complex Matrix에서는 Eigenvalue Problem을 풀었을 때, 복소수가 나온다면, 켤레복소수로 짝을 짓지 못할 수도 있다는 것을 말한다.
그런데, "특별한 경우"에는, Eigenvalue의 범위를 제한할 수 있다.
이러한 특별한 경우의 Matrix를 살펴보자.
1. (Hermitian)(에르미트 행렬)
먼저, 7-1에서 복소수벡터의 내적을 정의할 때, 다음과 같은 연산을 정의했었다.

실수벡터에서는 벡터도 행렬로 보고 내적을 다음처럼 정의했었다.

그럼, 복소수 벡터에서도 이러한 방식의 Notation을 사용하기 위해서 => Conjugate와 Transpose를 한번에 해주는 연산이 필요하다!
이를 염두하고 다음 연산을 정의하자.
1-1. 에르미트 연산

A에 Conjugate Transpose한 Matrix를 A의 Hermitian이라고 한다. (당연히 conjugate와 transpose의 연산순서는 상관이 없다.)
그러므로, 복소수벡터의 내적은 다음처럼 쓴다.

1-2. 에르미트 행렬(Hermitian)
그리고, A가 에르미트 행렬(Hermitian)이라는 말은

ex) 아래의 A는 Hermitian이다.

(NOTE)
에르미트 행렬의 대각성분은 당연히 "실수"이어야 한다!
(NOTE)
에르미트 행렬과 대응되는 실수행렬은 => 대칭행렬(Symmetric Matrix)이다! (실수는 Conjugate에 영향받지 않음)

2. Skew-Hermitian (반에르미트 행렬)
2-1. Skew-Symmetric (반대칭행렬)
"실수 행렬"에서 다음을 만족하는 행렬을 Skew-Symmetric이라고 한다.

2-2. Skew-Hermitian (반에르미트 행렬)
"복소수 행렬"에서 다음을 만족하는 행렬을 Skew-Hermitian이라고 한다.
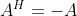
ex)

(NOTE)
반에르미트 행렬의 대각성분은 당연히 "Pure Imaginary(허수만 가짐)"이어야 한다!
3. Unitary Matrix(유니터리 행렬)
"복소수 행렬"에서 다음을 만족하는 행렬을 Unitary Matrix라고 한다.

즉, 실수 행렬에서 Orthogonal Matrix와 대응된다!!
다음 챕터에서 이 행렬들의 Eigenvalue가 어떻게 되는지 살펴보자!
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 13-1. Similarity Transformation, Change of Basis (0) | 2023.08.03 |
|---|---|
| (선형대수학) 12-2. Eigenvalue Problem of Complex Matrix (0) | 2023.08.02 |
| (선형대수학) 11-5. Application of Jordan Form - Differential Equation (0) | 2023.07.23 |
| (선형대수학) 11-4. Diagonalization (2) - Jordan Form (0) | 2023.07.19 |
| (선형대수학) 11-3. Application of Diagonalization - Differential Equations & Difference Equations (0) | 2023.07.17 |



