이번에는 Diagonalization을 어떻게 활용하는지에 대해서 살펴보자.
1. 상미분방정식 (Ordinary Differential Equation)
자세한 것은 추후 미분방정식 카테고리에서 보도록 하고, 여기서는 간단한 선형미분방정식의 풀이방법에 대해서만 생각해보자.
(a) 선형미분방정식(Linear Differential Equation)
=> 주어진 미분방정식 문제가 "선형사상"인 경우를 말한다.
=> 즉, 주어진 미분방정식을 "행렬"을 이용해서 다음과 같은 Form으로 나타낼 수 있다!

ex)

주어진 문제가 선형인 것을 알았으므로, 이를 위의 행렬 형식으로 고쳐보자!

(b) 이제 위의 선형미분방정식을 풀어보자!
먼저, Intuition을 얻기 위해서 다음과 같이 생각해보자..

=> Roughly, t에 대해서 미분을 했더니, 원래 함수(y_1,y_2)에 상수항만 곱해진다고 생각할 수 있다.
=> 그런 함수가 뭐가 있는지 따져보면...
=> Exponential 함수가 있다!!

그렇다면, 다음과 같이 x를 가정해 볼 수도 있을 것이다.

(z에는 최대 "상수배" 정도가 들어간다. 왜냐하면, z에 다른 t에 대한 함수가 들어가면, Exponential 함수로 가정한 이유가 없어진다.)
그러면, 우리 문제를 다음과 같이 표현할 수 있다.

즉, 저 z와 lambda에 대해서 Eigenvalue Problem을 푸는 문제로 바뀌었다!
그럼 Diagonalize를 통해서 미분방정식의 해를 구해보자!

=> 선형미분방정식의 해를 구했다!!
(물론, 저렇게 구한 해가 유일한 해인지(저 꼴로만 나와야 하는지...) 증명하는 것은 하지 않았다... => 추후 미분방정식 카테고리!)
(NOTE) Eigenvalue가 복소수인 경우
Characteristic Equation을 계산할 때, 다음과 같은 복소수 해(Eigenvalue)가 나온다고 하자.

A가 "실수"행렬이라고 하면, Characteristic Equation에서의 계수는 항상 "실수"가 나와야 한다. 그러므로, Conjugate 또한 Characteristic Equation을 만족한다. 즉, 다음 값도 Eigenvalue이다.

그러므로, 미분방정식의 Solution에는 다음과 같은 꼴이 나온다.

(c) 해를 관찰해보자!
해의 꼴이 Exponential 함수의 선형결합으로 나오는 것을 확인할 수 있다. (Eigenvalue가 중근이 나오는 것은 일단은 제외)
또한, 지수가 Eigenvalue인 것을 확인할 수 있는데, Eigenvalue가 "복소수"인 경우도 합해서 생각해보면
해에 대해서
=> (Eigenvalue의 실수부분 < 0) -> t가 커질수록 영향이 줄어든다!
=> (Eigenvalue의 실수부분 > 0) -> t가 커질수록 영향이 커진다!
즉, 이 미분방정식을 하나의 시스템으로 본다면
=> 시스템의 안정성을 확인할 수 있다.
(Stability of Differential Equation)
=> (모든 Eigenvalue의 실수부분 < 0) -> Stable!!
=> (어떤 Eigenvalue의 실수부분 > 0) -> Unstable!! ((NOTE) 어떤 것 하나라도 Unstable하면 전체가 Unstable!)
=> (모든 Eigenvalue의 실수부분 <= 0 ) -> Neutrally Stable!!
또한, Eigenvector는 영향을 주는 "방향(Direction)"으로 생각할 수 있다!! => Principal Axis!!
=> 선형(연속)시스템에서의 Stability 개념과도 연관이 있다!!!
2. Difference Equations(차분 방정식)
(미분방정식 -> Differential Equation, 차분방정식 -> Difference Equation)
Difference Equations란 쉽게 말해서 "점화식"을 생각하면 된다. 즉, Step by step으로 Solution을 구해가는 것이다.

앞에서 보았던 피보나치 수열을 행렬 형식으로 풀었던 것을 떠올리면 된다!!
이 외에도, 미분방정식을 수치적으로 풀 때 이용할 수 있는데, 한 예시로...

이를 행렬로 표시해보면...

복잡하긴 하지만, 이 경우에도 위의 경우와 마찬가지로 A의 Stability를 관찰해보면, 이렇게 수치적으로 구한 Solution이 발산하는지, 수렴하는지 판단할 수 있다!
(물론, 이 시스템 자체가 발산할 수도 있지만, 저 Time-step(Delta t)에 따라서도 Stability는 바뀔 수 있다!)
2-1. Markov Process
흔히 생물학이나 인문학에서 많이 사용하는 것으로 예시를 보면서 생각해보자..
ex)
하루에 한번씩 색을 바꿀 수 있는 식물이 있다고 하자. 이 식물은 빨간색 혹은 파란색으로 색을 바꿀 수 있다.
그런데, (빨간색 -> 파란색)으로 바뀌는 확률은 30%, (파란색 -> 빨간색)으로 바뀌는 확률은 10%이다.
처음에 이 식물을 관찰할 때, 빨간색 50, 파란색 50개가 있었다고 하면 (빨간색)과 (파란색) 식물의 비율은 어떻게 변할까???
이 경우도, Step by Step으로 점화식처럼 행렬로 표현할 수 있다!!
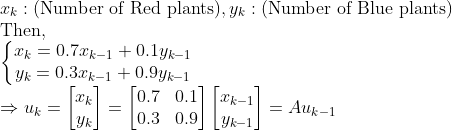
=> 이렇게, 각 Column의 합이 1이고(전체 총량은 변하지 않음), 각 성분이 음수가 아닌 경우
=> Markov Process라고 부른다!
그러면, 문제를 풀어보자!
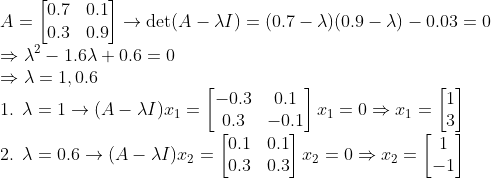


k가 커지면 (0.6)^k는 사라지므로, 결국 시간이 아주 많이 지나면
=> (빨간색 : 파란색 = 1:3) => (빨간색:25개, 파란색: 75개) 로 고정이 될 것이다!!!
=> 결국 시간이 흘러서 개수가 고정이 된다는 말은 이 시스템이 "Stable"이라는 말인데, 어디서 이를 알 수 있을까???
=> 사실, 다음 식에서 Stability를 알 수 있다!!

=> 왜냐하면, u를 w로 변환하는 과정 자체는 사실 T만 곱하면 되는 것이라 시간과는 관련 없다!
=> Stable하다는 것은
=> 저 지수 k에 의해서 "발산"하지 않는다는 것이다.

=> 이를 위해서는 결국...

이어야 Stable하다고 할 수 있다.
이를 Markov Process 말고도, 모든 Difference Equation으로 확장시킬 수 있다!!
(Stability of Difference Equation)
=> (모든 Eigenvalue의 절댓값 < 1) -> Stable!!
=> (어떤 Eigenvalue의 절댓값 > 1) -> Unstable!!
=> (모든 Eigenvalue의 절댓값 <= 1) -> Neutrally stable!!
=> 선형(Discreted)시스템에서의 z-transformation과도 연관이 있다!!!
여기까지, Diagonalization의 응용에 대해서 알아보았다.
=> 미분방정식과 차분방정식의 안정성!
선형시스템 카테고리를 보면 알겠지만, 중요한 개념이므로 꼭 알고가자!
지금까지는 Eigenvalue를 구할 때, "중근"이 나오는 경우를 자꾸 패스했는데, 이에 대한 내용을 다루어볼 것이다.
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 11-5. Application of Jordan Form - Differential Equation (0) | 2023.07.23 |
|---|---|
| (선형대수학) 11-4. Diagonalization (2) - Jordan Form (0) | 2023.07.19 |
| (선형대수학) 11-2. Diagonalization (1) (0) | 2023.07.17 |
| (선형대수학) 11-1. Eigenvalue Problem (0) | 2023.07.16 |
| (선형대수학) Summary 1. Ax=b를 어떻게 푸는가? (1) | 2023.07.16 |



