11-2에서 Diagonalization에 대한 이야기를 하면서
=> Repeated Eigenvalue에 대한 내용을 설명하였다. 이 때, 2가지 Case가 생기는데,
1. 중복되는만큼 Eigenvector를 찾을 수 있다!!! -> Diagonalization이 가능!
2. 중복되는만큼 Eigenvector를 찾을 수 없다!!! -> Diagonalization이 불가능!
(이 때, 중복된 Eigenvalue의 개수 : Algebraic Multiplicity라고 하고
linearly independent한 eigenvector의 개수 : Geometric Multiplicity(즉, Null Space의 Dimension)라고 한다.)
문제가 되는 경우는 2번 경우이다!!!
이 문제를 해결하기 위해서 "Diagonalization"이 아니라, 이와 비슷한(Similar) 모양을 가진 행렬로 Decompose하게 된다.
이 비슷한 모양을 바로 "Jordan Form"이라고 하고, 다음 모양이다.
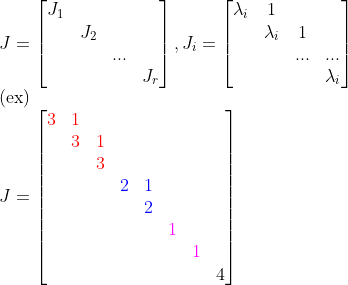
(뒤에서 설명을 하겠지만, 저기서 보라색의 1에 왜 1이 안 붙었냐면...?
=> 위의 1번 케이스인 경우! (다른 Eigenvector를 찾는 경우))
결국, Eigenvector만 다 다르게 찾을 수 있다면 => 그냥 대각행렬! (Eigenvalue Matrix!)
정리하자면,

Diagonalization은 Eigenvalue Problem으로부터 나왔다..
그러면, Jordan Form은 어디서부터 왔을까??
Jordan Form에서 Matrix Block 한 개만 가져와서 살펴보자.

=> 첫번째 식은 그냥 Eigenvalue Problem이지만, 두번째와 세번째 식은 약간 다르다! 저 식을 Generalized Eigenvalue Problem이라고 한다. 또한, 여기서 구한 Eigenvector를 Generalized Eigenvector라고 한다.
여기서 lambda와 x_1,x_2,x_3을 구한다고 해보자. 그러면 다음처럼 구하면 된다!
(a) Eigenvalue Problem을 풀어서 lambda와 x_1을 구하자!
(b) lambda와 x_1을 알기 때문에, 두번째 식에서 x_2를 구할 수 있다.
(c) 세번째 식에서도 같은 방법!! (Induction) -> Repeat!!
ex1)
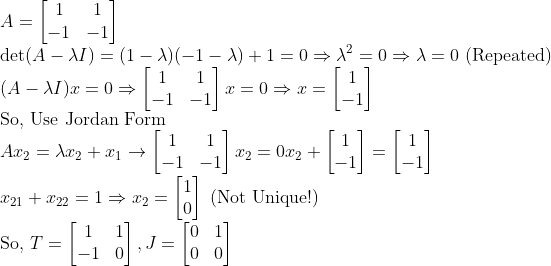
ex2) 조금 더 복잡해진 경우


여기서 x'의 a는 아무거나 들어가도 되므로, 그냥 0을 집어넣는다.
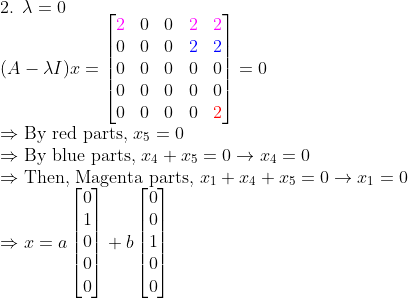

여기서도 x'의 c,d에는 아무거나 들어가도 되므로, 0을 넣는다.
그러므로, 정리하면
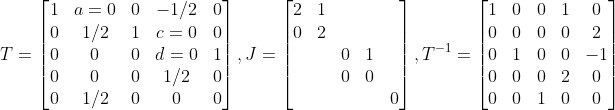

그런데, 모든 정사각행렬에 대해서 Jordan Form으로 변환할 수 있을까???
=> 결론적으로는
모든 정사각행렬 A가 저 Jordan Form 꼴로 변환이 된다
이를 증명하기 위한 과정은 다음과 같다.
(1) 일단 A를 위에서 나온 Jordan Form으로 쪼개버린다!
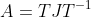
(2) 이렇게 쪼개버렸을 때 나오는 T와 J를 항상 구할 수 있다면 A는 항상 Jordan Form으로 쪼개질 수 있다는 것을 말한다.
(이 때, T가 Invertible해야 하므로, T를 구성하는 Column은 Linearly Independent이어야 한다.)
=> 증명 끝!
문제를 살펴보기 위해 같은 Eigenvalue를 가진 Matrix Block을 하나 가져와보자!
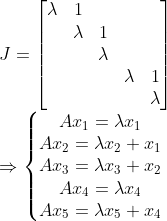
그런데, 여기서 한가지 살펴볼 점은 "(1) 모든 상황에서 실제로 저렇게 x_2,x_3...을 구할 수 있을까??, (2) 저 x들이 모두 Linearly Independent한가???" 이다. 이를 살펴보자.
(1) x를 구하는 방법!
위의 예시에서 x_1~x_3과 x_4~x_5를 사실 따로 볼 수 있을 것이다. 그러므로 하나의 String(즉, 따로 본 것 한 개)을 일반화해서 쓰면 다음과 같다. (Eigenvalue는 같지만, 여러개 Eigenvector를 가진다면 각각 다른 Block이라고 생각한다!)
=> 이러한 {x_1,..,x_n}을 Jordan Chain이라고 부른다.
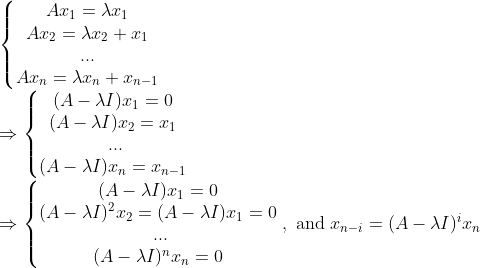
그러므로, x_n의 존재성만 알면, 나머지 벡터는 다 구할 수 있다.
첫번째 식은 그냥 Eigenvalue Problem이므로, lambda를 구할 수 있다. (x_1은 조금 나중에 구하자!) 특히, 다음 성질을 얻을 수 있다.

또한, 마지막 식을 생각해보면
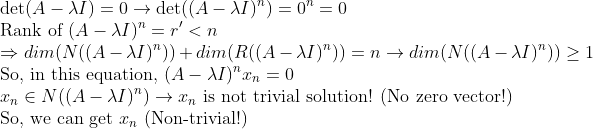
=> 그러므로, Zero-vector가 아닌 x_n을 구할 수 있고, 순차적으로 x_i를 구할 수 있다!!
=> 모든 상황에서 x_i를 구할 수 있다!
(2) 구한 x_i들이 모두 Linearly Independent함을 보이자!
이 경우에는 하나의 String으로 보는 것이 아니라 Eigenvalue가 같은 전체 Block을 보자! (즉, x_1~x_5를 하나의 묶음으로!)
위의 예시로 설명을 해보자...

그러면 다시 Index 역순으로 가보면

그러나, Index를 순차적으로 다시 올려보면

그러므로 다음과 같이 분류해볼 수 있다!
1. Generalized Eigenvalue Problem을 시작하는 Eigenvector -> Null Space와 Column Space에 동시에 속함!(*)
2. Generalized Eigenvalue Problem에 속하는 Eigenvector -> Column Space에"만" 속함!(**)
(만일, Generalized eigenvector가 Null Space에도 속해버린다면, 다음과 같은 상황이 펼쳐진다...)

3. 그냥 Eigenvalue Problem 하나(그냥 Diagonalzation) => Null Space에"만" 속함!(***)
ex)

=> 그러므로, x의 Linearly Independence는 Null Space와 Column Space에 달렸다는 것을 알 수 있다!!!
(2-a)
Null Space와 Column Space의 Intersection의 Dimension이 0(즉, 원점!)이라고 하자.

즉, Null Space와 Column Space에 동시에 속하는 Eigenvector가 없어야 한다.
=> 그냥 Diagonalization과 동일하다!! -> Eigenvector가 모두 Linearly Independent!
=> Index 역순으로 갈 때에, 첫번째 식이 "Column Space"에 속하는 것을 봤었다... -> 만약에 각각의 String이 1개만 있다면 Column Space에 속하는 것을 보일 수 없다!
(2-b)
Null Space와 Column Space의 Intersection의 Dimension이 p라고 하자.
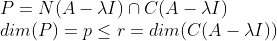
Column Space에서 Basis를 하나 잡으면 -> p개의 성분은 Null Space에 속함(*) / r-p개의 성분은 Null Space에 속하지 않음!(**)
=> Null Space에"도" 속하는 p개의 성분(벡터)를 각각 x_1,x_2,...,x_p라고 하자.(*)
=> 시작하는 Generalized Eigenvector를 뜻한다!
=> 나머지 r-p개의 성분(**)이 Column Space에 속하기 때문에 다음처럼 생각할 수 있다.

=> 즉, y_i들은 중간~끝 Generalized Eigenvector를 뜻한다!
이 때, x_i들이 모두 Linearly Independent하기 때문에, y_i들도 Linearly Independent하다.
(증명)

이를 다르게 보면, x_i들의 선형결합이 0이 되면 안되기 때문에(Linearly Independent) y_i의 선형결합 또한 Null Space에 있을 수 없다.
(증명)

또한, y_i는 Column Space에 있을 수 없다!
(증명)
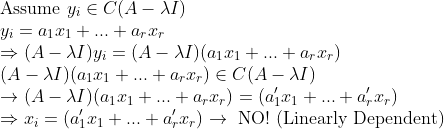
=> 그러므로, y_{p+1},....,y_r도 x_1,x_2,...,x_p와 Linearly Independent이다.
사실 여기까지만 하면, 저 Block에 대해서는 Basis를 구한 것이나 마찬가지이다.
=> 즉, 우리가 구한 Jordan Form의 (Generalized) Eigenvector들은 모두 Linearly Independent!
그러나, Diagonalized되는 것들도 생길 수 있으므로
마지막으로, Null Space에서도 마찬가지로, Null Space에"만" 속하는 Linearly Independent Vector들을 n-r-p개 뽑아낼 수 있다!! (Dimension of Null space = n-r) -> 이를 z_1,z_2,...,z_{n-r-p}라고 하자.
이를 다 모아놓으면...
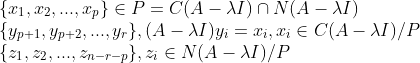

이렇게 구한 Eigenvector들은 x,y,z 모두 Linearly Independent한 것을 알 수 있다!! (사실, 각각 쪼개놓은 Vector Space에서 골라놓은 것이기 때문에 Linearly Independent하다고 할 수 있다!)
이러한 방법을 모든 Eigenvalue에 대해서 수행할 수 있으므로, 결국 모든 A에 대해서 T와 J를 구할 수 있다!!
이해를 위해서 ex2의 상황을 생각한다면
=> 같은 Eigenvalue에서만 생각해본다면!


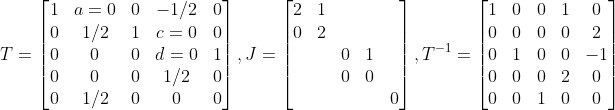
1. x_1,x_2,..,x_p => 그냥 Eigenvalue Problem을 풀어서 나오는 (Generalized 되어야 하는) Eigenvector x
([1 0 0 0 0])
2. y_{p+1},....,y_r => Generalized Eigenvalue Problem으로 나오는 Generalized Eigenvector
([0,1/2,0,0,1/2])
3. z_1,...z_{n-r-p} => Diagonalize가 가능한 Eigenvector
없음!
(NOTE)
eigvalue=2인 경우
Column Space -> [1 0 0 0 0], [0 0 0 1 1], [0 0 1 0 0]
Null Space -> [1 0 0 0 0]
=> P=[1 0 0 0 0]
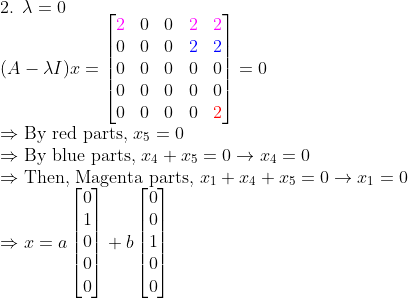

1. x_1,x_2,..,x_p => 그냥 Eigenvalue Problem을 풀어서 나오는 (Generalized 되어야 하는) Eigenvector x
([0 1 0 0 0])
2. y_{p+1},....,y_r => Generalized Eigenvalue Problem으로 나오는 Generalized Eigenvector
([-1/2 0 0 1/2 0])
3. z_1,...z_{n-r-p} => Diagonalize가 가능한 Eigenvector
([0 0 1 0 0])
(NOTE)
eigvalue=0인 경우
Column Space -> [1 0 0 0 0], [0 1 0 0 0], [0 0 0 0 1]
Null Space -> [0 1 0 0 0], [0 0 1 0 0]
=> P=[0 1 0 0 0]
(NOTE)
여기서 헷갈리면 안되는게
=> Eigenvalue Problem으로 나오는 것은
=> Generalized가 되어야 하는 Eigenvector + Diagonalize가 가능한 Eigenvector (즉, 1번+3번)
+추가!
(NOTE)
다음과 같은 관계를 Similar Matrix라고 한다.

(정리)
모든 행렬이 Jordan Form으로 나타낼 수 있다는 것을 증명하는 것은 꽤나 복잡할 수도 있지만, 어차피 사용하는 입장에서는 Jordan Form으로 어떻게 변형하는지만 알면 된다.
=> Generalized Eigenvalue Problem, Generalized Eigenvector!
다음 챕터에선 미분방정식에서 Repeated Eigenvalue의 궁금증을 약간 해소해줄만한 내용을 다뤄본다!
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 12-1. Complex Matrices (복소수 행렬) (0) | 2023.08.02 |
|---|---|
| (선형대수학) 11-5. Application of Jordan Form - Differential Equation (0) | 2023.07.23 |
| (선형대수학) 11-3. Application of Diagonalization - Differential Equations & Difference Equations (0) | 2023.07.17 |
| (선형대수학) 11-2. Diagonalization (1) (0) | 2023.07.17 |
| (선형대수학) 11-1. Eigenvalue Problem (0) | 2023.07.16 |



