바로 앞에서 Eigenvalue Problem에 대한 내용을 보았다.
Eigenvalue Problem은 다음과 같았다.

이 문제를 풀기 위해서 Characteristic Equation을 이끌어냈고, 다음과 같았다.

이 식이 n차 다항식이므로, 복소수관점에서 해가 총 n개가 나와야 한다!!!
=> Eigenvalue가 총 n개가 나온다! 각각에 해당되는 Eigenvalue와 Eigenvector를 다음과 같이 써본 후에 정리해보면

여기서 Eigenvalue로 이루어진 Lambda 행렬은 대각행렬(Diagonal Matrix)이다.
이렇게, A를 이용해서 Eigenvalue로 이루어진 Lambda 행렬(Eigenvalue Matrix라고 한다.)을 뽑아내는 과정을 Diagonalization(대각화)라고 한다.
또한, 여기서 T를 Eigenvector Matrix라고 한다.
여기서 몇 가지 궁금한 점이 생길 것이다.
1. Eigenvector Matrix T가 언제나 Invertible인가???
=> 답부터 얘기하면 "아니다!"
그러나, T가 Singular인 경우는 쉽게 나오지 않는다...
-> T가 Singular인 경우를 생각해보면, 결국 Eigenvector끼리 Dependent해야한다는 것이다.
(a) 모든 Eigenvalue가 다른 경우 (Distinct Eigenvalue)
=> 이 경우에는 Eigenvector가 Dependent할 수 없다.
(증명)


즉, Eigenvector들이 Linearly Dependent라는 조건을 가지고 가면 결국엔 a_1=0이 되어야 하는데, 이는 linearly dependent라는 것에 모순이다. 그러므로, 모든 eigenvector는 linearly independent
(b) 같은 Eigenvalue가 나올 때...
=> 이 경우에는 Eigenvector가 Linearly Independent일 수도, 아닐 수도 있다!!!
ex1) Diagonalizable

=> 이 경우에는 A-lambda I 의 Null Space의 Dimension이 다행히 2이므로, 2개의 Eigenvector를 뽑을 수 있다.
ex2) NON-Diagonalizable

=> 이 경우에는 A-lambda I 의 Null Space의 Dimension이 1이므로, 1개의 Eigenvector만 뽑을 수 있다.
=> Diagonalize를 위해선 2개의 Eigenvector가 필요한데, 하나가 모자른다...
=> Diagonalization을 할 수 없다!
=> Jordan Form의 등장! (다음 챕터)
2. Diagonalization을 어디에 쓰는가???
그냥 간단히 보면 LDU Decomposition과 크게 다를 게 없어보이나, Eigenvector Matrix의 특성 때문에, 제곱할 때 아주 편리하게 계산할 수 있다...

심지어 Eigenvalue Matrix는 대각행렬이므로, 그냥 성분을 k제곱 해주면 된다!
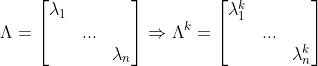
이를 이용해서 피보나치 수열의 일반항을 계산해보자!
ex) Fibonacci Sequence




=> 문제를 행렬표현으로 고쳐서 Diagonalize를 하면, 수열의 일반항을 구해낼 수 있다!!
=> x_0=0으로 하면 식이 더 간편해진다!
다음 시간에는 이 Diagonalize를 응용하는 것에 대해서 조금 더 살펴보자!
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 11-4. Diagonalization (2) - Jordan Form (0) | 2023.07.19 |
|---|---|
| (선형대수학) 11-3. Application of Diagonalization - Differential Equations & Difference Equations (0) | 2023.07.17 |
| (선형대수학) 11-1. Eigenvalue Problem (0) | 2023.07.16 |
| (선형대수학) Summary 1. Ax=b를 어떻게 푸는가? (1) | 2023.07.16 |
| (선형대수학) 10-3. Block Matrices -> Block Determinants (0) | 2023.07.14 |



