이번 챕터에서는 조금 더 DEEP한 행렬의 논의를 위해
Column Space, Row Space, Null Space 등의 개념들을 보도록 하자.
먼저, Subspace(부분공간)이라는 개념을 알고 가자.
물론, 추상대수학으로 가면, 더 포괄적인 정의가 있지만, 여기서는 "벡터공간"에서의 관점으로 접근한다.
(벡터공간의 부분공간(Subspace of a vector space))

그냥, 부분집합처럼 생각하면 되지만, 이 부분공간 또한 벡터공간이어야 한다는 조건이 있다.
그럼, 이제 행렬로 들어가서, 위에 나온 용어들을 정리해보자.
(각 벡터의 모양에 주의하자!!!)
(각 Space가 Subspace인지는 다 같이 맨 마지막에 살펴본다.)
1. (Column Space of A)
-> 말 그대로, A의 행(Column)벡터들이 만드는 Subspace이다. 이를 수식으로 표현해보면...

즉, Column Space는 A의 행벡터가 만드는 Linear Combination의 모음이라고 생각하면 된다.
또한, Column space는 다음과 같이 표현한다.

2. (Row Space of A)
-> A의 열(Column)벡터들이 만드는 Subspace이다. 이를 수식으로 표현해보면...

즉, Row Space는 A의 열벡터가 만드는 Linear Combination의 모음이라고 생각하면 된다. 또한, 다음과 같이 표현한다.

그런데, 식을 약간만 바꿔보면 Row space와 Column Space의 관계를 알 수 있다.

반대의 경우도 마찬가지로

라고 할 수 있다.
그러므로, 다음과 같은 식이 성립한다.

3. (Null Space of A)
-> 이번에는 관점을 달리해서, Ax=0을 만드는 벡터들에 대해서 생각한다.

즉, Null Space는 Ax=0의 해의 집합이라고 생각하면 된다. 그리고 다음과 같이 표현한다.

4. (Left Null Space of A)
-> Column Space와 Row space의 관계처럼, 이번에도, x가 왼쪽으로 오도록 한다.

또한, 위에서 Row space, Column space의 관계처럼 Left Null space도 다음과 같이 표현가능하다.

그러므로, Left-null space는 다음과 같이 표현한다.

이렇게 나온 4가지 Space가 subspace인지 살펴보자... 증명과정을 한번 살펴보는 것도 논리전개에 도움이 된다.
1. Column Space
(a) 벡터합에 대해서...
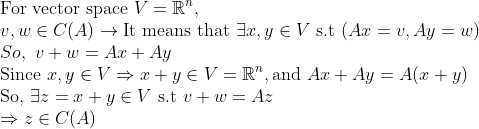
어려운 내용이 아니라서 이해하는 데에 무리는 없겠지만,
1. v,w가 Column Space에 있기 때문에 저런 x,y를 뽑을 수 있고,
2. x,y도 vector space의 원소가 되므로, 더해도 vector space의 원소가 된다
라는 식으로 논리를 전개하는 것은 알아두자.
(b) 스칼라 곱에 대해서

이번에도, 똑같은 방식으로 접근하면 된다.
=> Row space도 결국엔 같은 방식이므로 생략!
2. Null space
(a) 벡터합에 대해서...

(b) 스칼라곱에 대해서...

Null space의 경우에는 위보다 더 쉽다!
=> Left null space도 결국엔 같은 방식이므로 생략!
여기까지는 딱히 어려울 것도 없고, 무슨 의미가 있나 싶지만,
뒤에서 Ax=b를 풀 때에 꽤 좋은 Intuition(특히, Orthogonality에 관한 내용)을 주는데, 이 내용이 선형미분방정식에도 그대로 적용이 될 수 있기 때문에, 중요한 내용이 된다.
미분방정식에 대한 내용은 미분방정식 카테고리에서 하도록 하고,
다음시간엔 연립방정식을 푸는데에 일단 집중해보도록 하자.
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 4-3. Span, Basis, Dimension (0) | 2023.06.19 |
|---|---|
| (선형대수학) 4-2. Ax=b 풀어봅시다! (선형사상과 일반해, 특수해) (0) | 2023.06.18 |
| (선형대수학) 3. 벡터공간과 선형결합과 역행렬 (Vector Space, Linear Combination) (0) | 2023.06.15 |
| (선형대수학) 2-2. 가우스-조던 소거법 -> 역행렬의 존재성과 L(D)U Factorization (2) | 2023.05.25 |
| (선형대수학) 2-1. 역행렬을 쉽게 구해보자 (Gauss-Jordan Elimination) (0) | 2023.05.25 |



