이번 시간에는 선형대수학에서 아주아주 중요한 개념인 Linear Combination(선형결합)에 대해서 알아보도록 하자.
(참고링크)
(미적분학) 7-1. 역행렬을 위한 선형대수 기본 지식 (Linear Combination / Independence): https://0418cshyun.tistory.com/15
(미적분학) 7-1. 역행렬을 위한 선형대수 기본 지식 (Linear Combination / Independence)
(Note) 이번 챕터는 행렬의 기본적인 성질을 알고 있다는 가정 하에 작성하였습니다. 저번 챕터에서는 선형사상과 행렬 사이의 관계에 대해서 알아보았는데, 이번에는 조금 더 선형대수학 쪽으로
0418cshyun.tistory.com
가장 먼저, 벡터(Vector)가 무엇인지 정의해보자.
-> 단지, (스칼라) + (방향)이라는 애매한 물리적 정의 말고, 좀 더 수학적으로 다가가보자.
-> 정확한 이해를 위해선 추상대수학 내용을 참고하면 된다.
먼저, 벡터공간(Vector Space)에 대해서 정의하자.
(벡터공간(Vector Space))
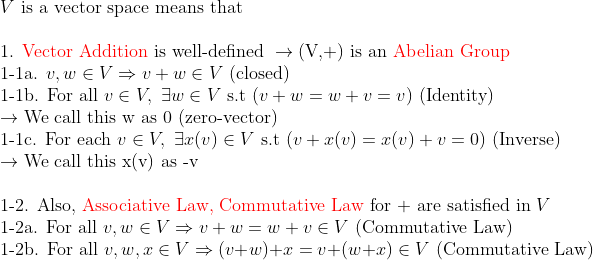

뭐가 이렇게 많냐고 생각할 수 있지만, 보면 별거 없다...
복잡하다면, 다음만 보면 된다.
=> 간단하게 벡터 합(Vector Addition)과, 스칼라 곱(Scalar Multiplication)이 잘 정의되어 있는 공간을 그냥 벡터공간이라고 한다.
추가적인 설명은 아래를 펼쳐보자!
좀 더 자세히 설명하자면,
1. 벡터합에 대해서
1-1a. 두 원소를 더했는데 집합 밖의 것이 나오면 안된다! => Closed...
=> 아주아주 예전에 "연산이 닫혀있다" 라는 개념을 들어본 적이 있을 것이다! => 사실, 아주 직관적이나 Powerful한 개념이다... (추상대수학에서 자세히 설명)
ex) 유리수 벡터를 더했더니 무리수 벡터가 나오는 일은 없다!
1-1b. 벡터합에 대해서 항등원(Identity)이 존재한다. (이 때, 항등원은 영벡터(zero-vector))
(Note) 위에서 0을 그냥 숫자 0 혹은 (0,0,0...)으로 생각하지 말고, v,w 처럼 V의 원소처럼 생각하자!
1-1c. 벡터합에 대해서 각 벡터마다 역원(Inverse)이 존재한다.
1-2. 또한, 벡터합에 대해서, 결합법칙과 교환법칙이 성립해야 한다.
1-2a. 벡터합에 대한 교환법칙
1-2b. 벡터합에 대한 결합법칙
이 때, 1-1a,b,c + 결합법칙(1-2b)를 만족하는 집합과 연산관계( (V,+) )를 "군(Group)"이라고 하고,
여기에 추가적으로 교환법칙(1-2a)를 만족하면 "아벨군(Abelian Group) 혹은 가환군"이라고 한다.
(NOTE)
교환법칙은 꽤나 특별한 성질로 생각해야 한다! -> 행렬의 곱을 생각해보자!
=> 결론은, 벡터합에 대해서 이 집합 V가 아벨군이면 된다!
2. 스칼라곱에 대해서,
2-1a. 닫혀있다.
2-1b. 항등원 존재(이 때, 항등원은 1)
2-2a. 스칼라곱에 대한 결합법칙
2-2b. 스칼라곱에 대한 분배법칙
=> 결론은, 스칼라곱에 대해서 이 집합 V가 잘 정의되어 있으면 된다!
그리고, 이 벡터공간의 원소를 벡터(Vector)라고 한다.
또한, 행렬에서 벡터에 관한 정의를 보면...
(행벡터(Column Vector)와 열벡터(Row Vector))

그러면, 선형결합(Linear Combination)에 대해서 알아보자.
벡터는 벡터합과 스칼라곱에 대해서 잘 정의되어 있으니, 다음과 같은 논의가 가능할 것이다!
(선형결합(Linear Combination))
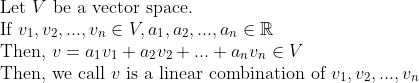
심플하게, 벡터 합과 스칼라 곱을 이용해서 만든 벡터라고 생각하면 될 듯하다.
이번에는 반대로 어떤 벡터 v가 벡터공간 V 안에 주어져 있다고 생각해보자.
그리고, 이번에도 n개의 벡터 v_1,v_2,..,v_n을 잡아서 v를 만들어본다고 하자...
그런데, 스칼라곱과 벡터합을 아무리 잘 뒤섞어서 계산해도 v가 안 만들어 질 수 있다.
ex)

이러한 관계를 선형독립(Linearly Independent)라고 한다.
그리고, 선형독립이 아니면(즉, v를 만들 수 있으면) 선형종속(Linearly Dependent)이라고 한다.
이 정의를 좀 더 수학적으로 써보면
(선형독립, 선형종속) (Linearly Independent / Dependent)
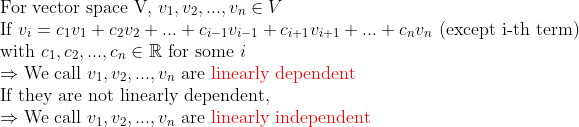
이 정의는 아주아주 중요하니 꼭 기억하자!!
이 정의가 왜 중요한지 가우스-조던 소거법에서 생각해보자.
1. 먼저, 위의 선형결합을 "행렬표현"으로 생각해보자.
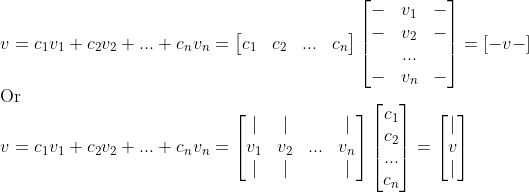
즉, 선형결합을 행벡터나 열벡터로 나타낼 수 있다.
더 나아가서, 행렬 곱 결과는 선형결합 벡터들의 List로 나타낼 수 있다. 즉,
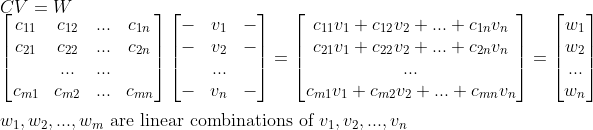
또한, 우리가 가우스-조던 소거법에서 Triangle matrix를 만들기 위해 했던 모든 연산들은 행렬곱이었기 때문에, 역행렬을 만드는 연산 결과도, 결국에는 원래의 행렬의 "선형결합" 벡터를 만드는 것과 동일하다.
즉,
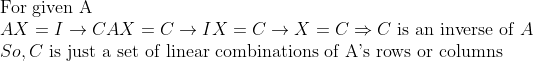
그런데, 우리가 중간에 역행렬이 못 나오는 조건을 살펴보았다.
=> 연산하다가 그냥 두 row나 column이 같아져서 0으로 그냥 쭉 행렬값이 밀리면... => 역행렬이 없었다!
2. 또한, linearly Independent와 Dependent에 대해서 조금만 더 생각해보자.
-> 만일, linearly dependent이면...
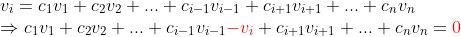
즉, 연산하다가 0으로 쭉 밀리는 상황이 나올 수 있다는 것이다.
-> 반대로, linearly independent이면...
이러한 일이 절대로 일어나지 않기 때문에, 연산하다가 0으로 밀리는 일이 없다!
이 두가지 개념을 잘 생각해보면
역행렬이 없다는 말은 -> 결국 역행렬을 계산하는 연산 도중에 0으로 밀린다!
-> 이 말은, 역행렬(정확히 말하면, 도중의 연산 결과)을 구성하는 row나 column벡터가 "선형종속(Linearly Dependent)"이라는 것을 말한다.
=> 이 말을 다시 생각하자면, 원래 행렬 또한 row나 column벡터가 "선형종속(Linearly Dependent)"이라는 것을 말한다.
결론은
어떤 행렬 A의 역행렬이 존재하지 않는다 -> 행렬 A의 열벡터나 행벡터가 선형종속!(Linearly Dependent)
어떤 행렬 A의 역행렬이 존재한다 -> 행렬 A의 열벡터나 행벡터가 선형독립!(Linearly Independent)
이러한 개념은 정사각행렬이 아닌 행렬의 역행렬을 생각할 때에도 중요하다.
ex)
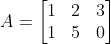
행벡터(Column)에 대해서 생각해보면, 2차원 벡터가 3개 존재한다... => 항상 Linearly Dependent가 된다!!!
심지어, 이러한 성질은 저 숫자(행렬의 원소) 때문이 아니라는 것을 금방 알 수 있을 것이다.
=> 좌우로 길쭉한 행렬말고도, 위아래로 길쭉한 행렬도 동일하게 Linearly Dependent가 되는 것을 알 수 있다!
그러므로, 이렇게 정사각행렬이 아닌 행렬의 역행렬은 존재하지 않는다고 할 수 있다.
(유사개념으로 Pseudo-Inverse라는 게 있긴 하지만, 역행렬과는 다르다!)
또한, 앞의 Rank 개념과 엮어서
-> (Rank) = (Linearly Independent한 벡터의 최대 개수)
로 생각할 수도 있다.
이는 뒤에 나올 Column Space, Row space, Dimension 등의 내용에서 차차 살펴보도록 하자.
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 4-2. Ax=b 풀어봅시다! (선형사상과 일반해, 특수해) (0) | 2023.06.18 |
|---|---|
| (선형대수학) 4-1. 여러가지 Subspace (Column / Row / Null / Left Null Space) (1) | 2023.06.15 |
| (선형대수학) 2-2. 가우스-조던 소거법 -> 역행렬의 존재성과 L(D)U Factorization (2) | 2023.05.25 |
| (선형대수학) 2-1. 역행렬을 쉽게 구해보자 (Gauss-Jordan Elimination) (0) | 2023.05.25 |
| (선형대수학) 1. 선형대수학의 1차 목표는???(What is the goal of Linear Algebra?) (0) | 2023.05.25 |



