역행렬이 있다는 가정하에서, 역행렬을 구해보자!
1. 2 by 2 행렬
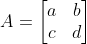
그러면, 역행렬은 이미 알고 있듯이,
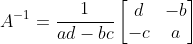
일 것이다. 이 식이 어떻게 나왔는지 살펴보자.
(증명 1) -> 단순 계산!
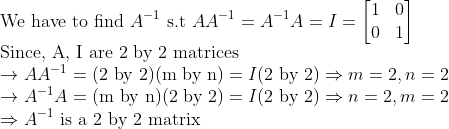
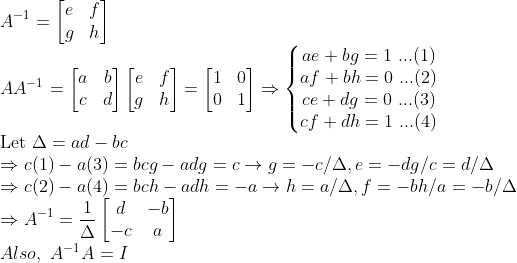
(NOTE)
만일 A가 정사각행렬이 아니면, 일단 항등원 계산부터 문제가 생긴다 -> 왼쪽에 곱할 때와, 오른쪽에 곱할 때 모양이 달라진다!!
(NOTE 1)
위의 증명에서, 잘 살펴보면... (1)(3), (2)(4) 이렇게 -> 그냥 두 개의 연립방정식으로 쪼갤 수 있다!!!
그러므로, 이런 식으로 쪼갤 수 있다.
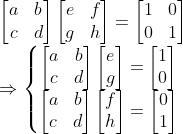
더 일반적으로,
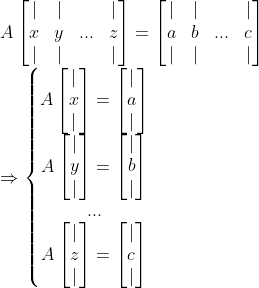
=> 행렬의 곱을 Column-wise으로 쪼갤 수 있다!!
(NOTE 2)
더 나아가서,
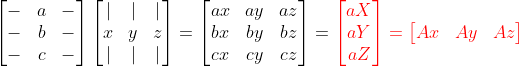
=> 행렬의 곱을 Row / Column연산으로 쪼개서 나타낼 수 있다는 것을 꼭 알고 있자!
위 (증명 1)에서 계산할 때, 결국 연립방정식에서 변수 e, f를 지워서 계산한다는 것을 알 수 있다.
=> 이러한 변수 제거방법을 이용해서, 일반적으로 역행렬을 계산하는 Gauss Elimination에 대해서 알아보자!
(Gauss(-Jordan) Elimination)
간단하게 예시로 알아보자.
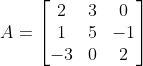
그러면, 여기서 X를 역행렬이라고 생각해보자! 즉,
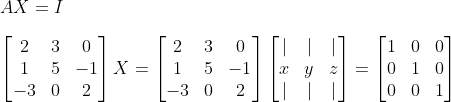
여기서 A를 I로 잘 바꾼다면, X=... -> 역행렬 X를 구할 수 있을 것이다!!
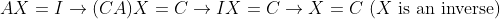
어떻게 I로 바꿀까? -> Column / Row 연산을 잘 이용하자!
(A의 i번째 row -> (i)라고 지칭하자)
A를 I로 바꾸기 위해서 ->
1. 성분을 0을 만들어 주자!
1.
먼저, [1 5 -1] -> 첫번째 숫자를 0으로 고치자!
어떻게??? -> 위에서 변수 없애는 것처럼!!!
=> (1)-2(2) = (2x+3y+0z)-(2x+10y-2z) = (1 0 0) - (0 2 0) = (0 -1 0)
=> (0x-7y+2z) = (0 -1 0)
그러면, 다음처럼 고칠 수 있다!
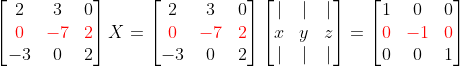
2. 세번째 줄 [-3 0 2] -> 첫번째 숫자를 0으로 고치자!
=> 3(1)+2(3) = (6x+9y+0z)+(-6x+0y+4z)=(3 0 2)
=> (0x+9y+4z)=(3 0 2)

3. 세번째 줄 [0 9 4] -> 두번째 숫자를 0으로 고치자!
=> 9(2)+7(3) = (0x-63y+18z)+(0x+63y+28z) = (0 -9 0) + (21 0 14)
=> (0x+0y+46z) = (21 -9 14)
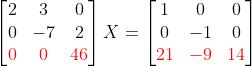
여기까지의 과정을 Gauss Elimination(가우스 소거법)이라고 하고,
특히, 저 대각선 성분들 (2, -7, 46)을 Pivot이라고 한다.
그리고, 여기서 나오는 A의 꼴을 보면, 위의 삼각형부분만 제외하고 나머지는 모두 0이다.
-> 이를 Upper Triangular Matrix라고 한다. (반대는 Lower Triangle)
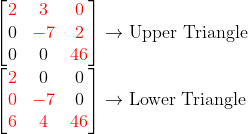
즉, 가우스 소거법은, A를 Upper Triangle을 만들어주는 방법으로 볼 수 있다.
2. 대각선의 성분들을 다 1로 바꾼다!
-> 대각선의 있는 성분으로 각 Row / Column 을 나눠주면 된다!
(NOTE) 만약에 대각선에 있는 성분이 0이면...??? => 역행렬의 존재조건이 된다! -> 다음 챕터!
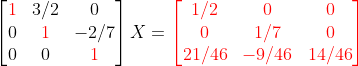
3. 아래부터 차근차근 올라가면서, Upper Triangle에 있는 성분들을 0으로 제거한다.
1. 두번째 줄 [0 1 -2/7]에서 -2/7을 0으로 바꾼다!
=> (2)+2/7(3) = (0x+1y-(2/7)z)+(0x+0y+2/7z) = (0+(2/7)*(21/46), 1/7+(2/7)*(9/46), 0+(2/7)*(14/46))
=> (0x+1y+0z) = (3/23, 32/161, 2/23)
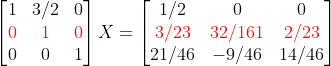
2. 첫번째 줄 [1 3/2 0]에서 0 -> 0으로 바꾼다! 그러나, 이미 0이므로 그냥 냅둔다.
3. 첫번째 줄 [1 3/2 0]에서 3/2 -> 0으로 바꾼다!
=> (1)-3/2(2) = (1x+3/2y+0z)-(0x+3/2y+0z) = (1/2-(3/2)*(3/23), -(3/2)*(32/161), -(3/2)*(2/23))
=> (1x+0y+0z) = (7/23, -48/161, -3/23)
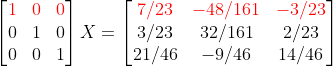
여기까지의 과정을 Gauss-Jordan Elimination(가우스-조던 소거법)이라고 한다.
그러므로 우리가 구하고자 하는 역행렬은
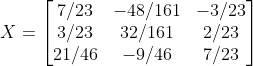
이 된다.
이 방법을 이용한다면, Ax=b의 해를 쉽게 구할 수 있다!

(그냥 I가 b로 바뀌었을 뿐!!!)
-> A를 I로 바꾸었을 때, 오른쪽 항에 남아있는 것이 해가 될 것이다!!!
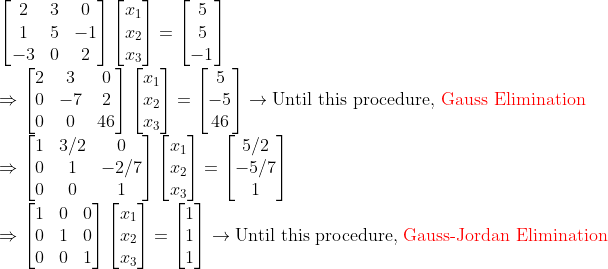
또한, 이 방법은 굳이 정사각행렬이 아니어도 사용할 수 있다!! (물론, 역행렬은 아니겠지만...)
ex1) 부정형(좌우로 길쭉)
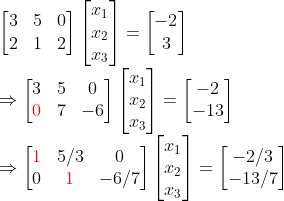
이 때... -> 부정형 -> 남는 변수 정해주어야 "하나의 해"를 구할 수 있다!
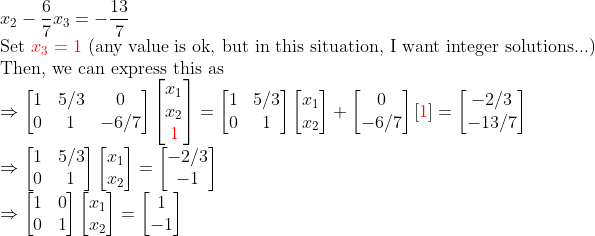
ex2) 위아래로 길쭉
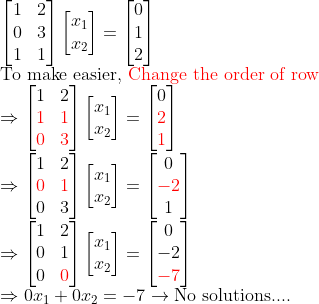
여기까지, 가우스-조던 소거법이 무엇인지, 어떻게 하는지 과정을 알아보았다.
그러나, 여기서 역행렬의 존재성이라던지 짚고 넘어가야 할 것들이 아주 많다. 이러한 내용들은 다음 시간에 알아보자!
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 4-1. 여러가지 Subspace (Column / Row / Null / Left Null Space) (1) | 2023.06.15 |
|---|---|
| (선형대수학) 3. 벡터공간과 선형결합과 역행렬 (Vector Space, Linear Combination) (0) | 2023.06.15 |
| (선형대수학) 2-2. 가우스-조던 소거법 -> 역행렬의 존재성과 L(D)U Factorization (2) | 2023.05.25 |
| (선형대수학) 1. 선형대수학의 1차 목표는???(What is the goal of Linear Algebra?) (0) | 2023.05.25 |
| (선형대수학) 선형대수학 개요 (0) | 2023.03.27 |



