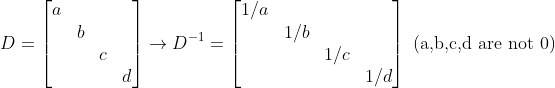지난 시간에는 가우스-조던 소거법에 대해서 살펴보았는데, 못 짚었던 내용들을 보자.
1. 역행렬의 존재 조건
=> 만일 위 과정에서 Pivot에 0이 포함된다면...
=> 대각성분을 1로 만들어 줄 수 없다!!!
=> 이 말은 사실, 하나의 줄이 다 0을 가지고 있다는 말이다!!!
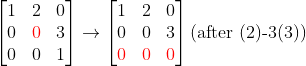
-> 우변에 해당하는 줄이 0(혹은 [0, 0, ... , 0])이 아닌 이상, 이 문제를 해결할 수 없다. 즉, 해가 존재하지 않으므로 역행렬도 없다!
(NOTE)
그렇다면, 만약에 우변에 해당하는 줄이 0이라면...??
-> 우리가 가지고 있는 행렬에서 그 줄을 빼도 된다는 말과 동일하다! -> 어차피 0=0이니, 아무 의미 없는 row이다!
-> 즉,
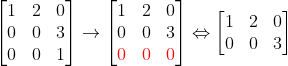
이런 식으로 그냥 행렬을 줄여줄 수 있다!!
(NOTE)
이런 식으로, 행렬이 가지고 있는 "실제 정보"의 개수를 Rank라고 할 수 있다.
-> 즉, 위에서는 rank=2 ([0,0,0]은 아무 의미 없다!)
-> 또한, 나중에 나올 Column space, Row space등과 엮여서, 행렬의 Dimension으로 볼 수도 있다. 즉, 위에서 dim=2...
(NOTE)
역행렬을 가지기 위해선, 정사각행렬 + Full-rank(즉, 행렬의 row/col 개수와 rank가 일치해야 한다!)
2. 행/열 연산을 그대로 명시해서 써줄 수는 없는가?? -> Decomposition
Gauss-Jordan 소거법을 이용할 때, 행에 대한 연산과, 그 결과를 알맞은 행에 넣는 방식으로, 계산을 했는데, 이러한 연산과정을 좀 명시적으로 적어줄 수는 없을까?
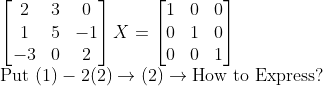
위에서 본 내용을 다시 살펴보자...
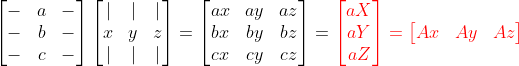
이를 이용해준다면
(첫번째 행)-2*(두번째행) -> (두번째행)에 대입!
이라는 연산을
이렇게 행렬곱으로 나타내줄 수 있다!!!
=> 행 연산을 행렬곱으로 나타낼 수 있다!
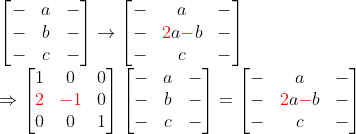
또한, 위의 예시(위아래로 길쭉한 것의 가우스 소거법)에서, 계산 편의를 위해서, 행의 위치를 바꿨다.
-> 이러한 행의 자리바꿈도 당연히 행렬곱으로 나타낼 수 있다!
이렇게 행의 자리를 바꿔주는 matrix를 Permutation Matrix라고 한다.
그렇다면, 맨 처음으로 돌아가서 Gauss-Jordan 소거법을 각 단계마다, 행 연산을 계속 명시적으로 쓴다면....
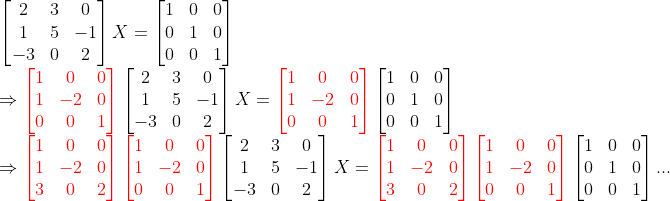
(+)
거기에 더해서
Lower Triangle끼리만 곱하면 -> Lower Triangle이 나오고,
Upper Triangle끼리만 곱하면 -> Upper Triangle이 나온다!!!
=> 이는 단순 계산이니, 직접 해보면 느낌이 온다!
그러면 결국에는 가우스 소거법의 결과는 다음과 같다.
(2-1의 예시에서 1번과정까지의 결과!)
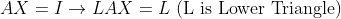
(이 때, 행의 순서를 바꾸면, Lower Triangle이 당연히 깨질텐데, 그렇게 되지 않도록 A를 잡아버리자! (미리 A의 행 순서를 Lower Triangle을 해치지 않도록 바꿔버리자!))
게다가, 가우스 소거법의 결과로 위에서 LA는 Upper Triangle이 된다!
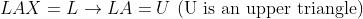
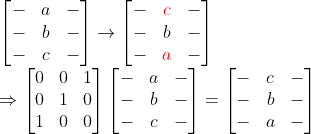
이어서 가우스-조던 소거법까지 가보면... (여기서, 대각성분이 0인 것은 일단 무시하자.)
(2번과정 -> 대각성분을 1로 만들기!)
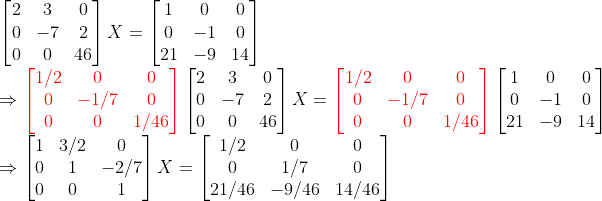
-> 저기서 저 빨간 행렬은 대각선 성분만 살아있다! (대각선 성분만 가진 행렬을 대각행렬(Diagonal Matrix)이라고 한다.)
정리하면,
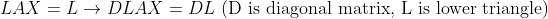
나머지 3번과정까지 생각해본다면... -> Upper Triangle 성분을 0으로 만들어준다!
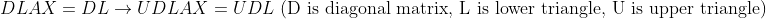
이러한 과정을 거치면, 결국 가우스-조던 소거법의 결과에 따라서
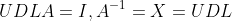
가 된다.
게다가, 대각선 성분이 0이 아니라는 가정만 하면
Upper Triangle의 역행렬 / Lower Triangle의 역행렬은 항상 존재하고,
(Upper Triangle의 역행렬) = (Upper Triangle)
(Lower Triangle의 역행렬) = (Lower Triangle)
이 된다!
(증명)
Upper Triangle인 경우에만 생각해보자. (대각성분은 위에서 했던 것처럼 대각행렬로 생각하면 된다!)
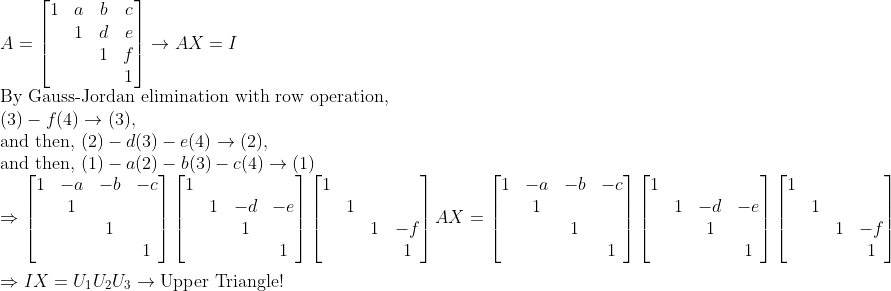
또한, 대각행렬은 (대각성분에 0만 없으면) 역행렬을 가진다!
(증명)
이러한 결과에 따라서...
1. 가우스 소거법은
A를 (Lower Triangle), (Upper Triangle)로 나누는 방법으로 볼 수 있다! -> LU Decomposition
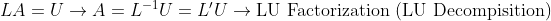
2. 가우스-조던 소거법은
A를 (Lower Triangle), (Diagonal Triangle), (Upper Triangle)로 나누는 방법으로 볼 수 있다! -> LDU Decomposition
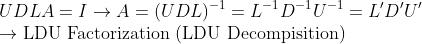
단, 이 경우에는 D의 대각성분에 0이 포함되어서는 안된다!(Pivot이 0이 되면 안된다) -> 역행렬의 존재조건과 일치!
LDU Decomposition이 가능(대각성분에 0 없이) <-> A의 역행렬이 존재한다!
(NOTE)
행의 자리바꿈까지 같이 합쳐서 생각해본다면 (Permutation을 고려하면)
LDU Decomposition은 다음과 같이 쓸수 있다!!
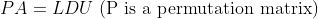
3. 연산시간??
A를 n by n 행렬이라고 하자.
(a) LU Decomposition
-> 기본 A에서, Lower Triangle자리에 있는 성분들을 0으로 만들어줄 때마다, 행 연산(혹은, 행렬곱)을 해주어야 한다.
-> 행 연산은 연산횟수가 n번이 될 것이다. (0은 연산 제외해줘도 되는 것을 고려해보자!) -> k
-> 그러므로, Lower Triangle 자리에 있는 성분들을 모두 0으로 만들어주려면 (lower triangle 자리 개수)*(행 연산의 연산횟수)만큼의 연산을 해주어야 한다. 즉,
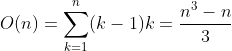
번의 연산이 필요하다.
그러면, 행 연산 과정에서 L을 알 수 있고, U도 행연산의 결과값으로 알 수 있으므로, LU Decomposition이 완료된다.
(b) LDU Decomposition
-> 위의 LU Decomposition을 끝낸 뒤에, 각 열의 값을 대각성분(Diagonal)으로 나누어주어야 한다.
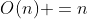
-> 그리고, 대각성분들의 값으로 Diagonal Matrix를 만들면, LDU Decomposition이 완료된다!
=> 결국 연산 Order는
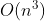
정도가 될 것이다!
여기까지, 가우스-조던 소거법에 대해서 알아보았다.
꽤 자세히 설명을 하였으니, 도움이 되기를 바란다.
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 4-1. 여러가지 Subspace (Column / Row / Null / Left Null Space) (1) | 2023.06.15 |
|---|---|
| (선형대수학) 3. 벡터공간과 선형결합과 역행렬 (Vector Space, Linear Combination) (0) | 2023.06.15 |
| (선형대수학) 2-1. 역행렬을 쉽게 구해보자 (Gauss-Jordan Elimination) (0) | 2023.05.25 |
| (선형대수학) 1. 선형대수학의 1차 목표는???(What is the goal of Linear Algebra?) (0) | 2023.05.25 |
| (선형대수학) 선형대수학 개요 (0) | 2023.03.27 |