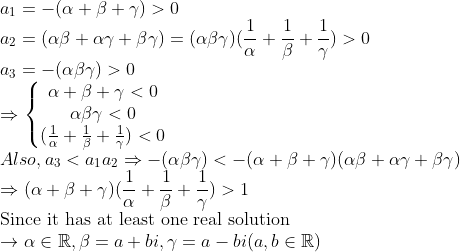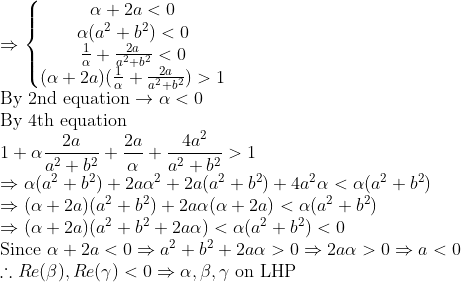(참고!)
(선형시스템) 1-3. 전달함수와 Pole, Zero (Transfer Function, Pole, Zero): https://0418cshyun.tistory.com/118
(선형시스템) 1-3. 전달함수와 Pole, Zero (Transfer Function, Pole, Zero)
이번에는 LTI 시스템의 전달함수만 따로 떼어서, 조금 더 살펴보도록 하자. (Transfer function and Impulse) 앞에서 본 바와 같이, 라플라스 변환을 이용하면 그러므로, 예를 들어서 시스템에 뭐 망치로
0418cshyun.tistory.com
이번엔 LTI system의 안정성에 대해서 알아보자.
"선형"시스템이니, 안정성도 두개로 쪼개서 알아볼 수 있을 것이다.
1. 오로지 Input에 의한 안정성(Zero-state Stability) (이렇게 쓰긴 했지만, 시스템이 분명히 관여는 할 수밖에 없다.)
2. 오로지 시스템 자체에 의한 안정성(Zero-input Stability)
예를 들어서,
1번의 경우 - 비행기가 안정되어 있는데, 내가 Full-Throttle을 주면, 어떤 반응을 하는지? (발산하는지?)
2번의 경우 - 비행기가 Roll=70deg로 틀어져 있는데, 가만히 놔두면 이게 알아서 수평을 찾는지 본다고 생각하면 된다.
먼저, 오로지 Input에 의한 안정성인 BIBO Stability에 관해서 알아보자!
(BIBO Stability) -> Bounded-Input Bounded-Output Stability
(시스템의 Initial Condition이 Relaxed되었을 때, Zero-State) Bounded Input을 주면, Bounded Output이 튀어나온다는 것을 보장한다!
-> 즉, "INPUT"에 따른 반응을 보는 것이다.
1. SISO
시스템의 Response(Output)이 다음과 같이 계산되었던 것을 생각해보자!

어차피 u는 Bounded이고, 그러면 저 g가 "적분"관점에서 Bounded 되어 있으면 Response는 Bounded 될 것이다!
즉,
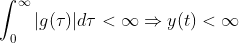
임은 자명하다! (여기서 g가 Impulse Response였다는 것을 기억하자!)
그리고, 저 식을 만족하기 위해선 t가 infinity로 갈 때, g는 0으로 수렴해야 할 것이다!
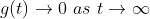
게다가, 여기에 더해서, 1-3에서 보았던 그래프들을 보면
-> Pole이 (실수부분이 음수이면) -> 즉, LHP(Left-Half Plane)에 있으면 -> Stable!
-> Pole이 (실수부분이 양수이면) -> RHP(Right-Half plane)에 있으면 -> Unstable!
-> Pole이 Imaginary-axis에 걸려있으면 -> 진동!
하는 것을 볼 수 있었다.
(Pole and BIBO Stability)
어떤 시스템이 Proper Transfer Function을 가질 때,
BIBO Stable <=> 모든 Pole이 LHP 내부에 존재해야 한다!
(단, 여기에는 Proper Transfer Function이어야 한다는 가정이 필요하다.... 왜냐하면, 만일 Improper일 때, s가 infinity가 되면, Impulse Response가 무조건 Infinity로 가야 하기 때문이다 -> 위의 BIBO Stable 조건을 만족할 수 없다.)
2. MIMO
이 경우에도
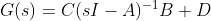
이기 때문에, 결국 SISO와 똑같이 생각할 수 있지만,
SISO의 경우 -> 저 (sI-A)의 역행렬 -> det(sI-A)=0 -> Eigenvalue가 모두 POLE이 된다! (그냥 일변수이므로, 저 역행렬은 분모로 들어간다.)
MIMO의 경우 -> det(sI-A)=0 -> Eigenvalue가 모두 POLE이 아닐 수 있다!!!
왜냐하면, 저 역행렬을 구하는 와중에 분자분모가 지워질 수 있기 때문이다!
-> 그러므로, BIBO Stable이라고 모든 Eigenvalue가 모두 LHP에 있지는 않다.
하지만, 어차피 지워지는 것을 생각해서 Pole을 정의하기 때문에, Pole의 정의를 사용하면 별 상관이 없다.
즉, 이것만 조심하면, 그냥 SISO와 동일하게 생각할 수 있다.
이번에는 그냥 저 시스템 자체(Zero-Input)의 안정성 -> Internal Stability 을 보자.
이 경우에는 시스템에서 u를 지워버리면 되므로,
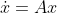
의 안정성만 보면 된다. (물론, MIMO라는 것을 잊지 말자!) 이 방정식의 해는
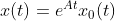
인 것을 알고 있으므로, 이에 대한 분석만 해주면 될 것이다.
(Lyapunov Stability)
만일, 위에서
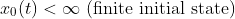
일 때,
1. Bounded Response를 주면 -> (Marginally) Stable (in the sense of Lyapunov)
2.
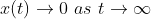
즉, 시간이 지나면, 0으로 수렴하는 Response를 주면 -> Asymptotically Stable이라고 한다!
(왜 Lyapunov라는 이름이 붙었는지는 다음 시간에!)
사실, 위의 BIBO Stability에서 그냥 u=0으로 준다고 생각할 수도 있으므로,
-> Pole(여기선 A의 Eigenvalue가 될 것이다.)이 모두 LHP 내부에 있다면 Asymptotically Stable일 것이다!
종합해보면, 결국 이 Pole이 LHP에 있는 것이 중요하단 것을 알 수 있을 것이다!
이를 쉽게 알 수 있는 방법 중의 하나가 Routh Test이다.
LTI System에서, 결국에 Pole에 관여하는 방정식은 바로 이 특성방정식(Characteristic Equation)이다!
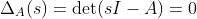
이 특성방정식의 해가 결국엔 Pole이 된다.(물론, MIMO의 경우 Cancellation이 있을 수 있다.)
그런데, A가 2 by 2이면 구하기 쉬울텐데, n by n이면 특성방정식이 n차방정식이 되어 해를 구하기 어렵다...
그러면, 이 해를 좀 쉽게(물론 딱 떨어지게는 아니겠고), 적어도 어디 근처에 있는지 알 수 있는 방법이 없을까? -> Routh Test
(Routh Test)
여기선 방법만 소개하고 자세한 내용은 Advanced에 추후 올릴 예정!
특성방정식의 최고차항 계수를 1로 만든 후에 생각한다.
특성방정식의 해를 alpha, beta,... 라고 한다면 이 해들이 모두 LHP에 있으려면
1. 이차방정식
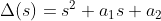
근과 계수와의 관계를 이용한다면
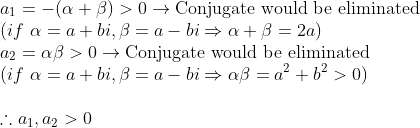
이면 된다!
2. 삼차방정식
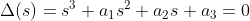
근과 계수와의 관계를 이용한다면

이면, 모든 해가 다 LHP에 존재한다.
(NOTE)
그냥 각 계수가 0보다 크다 가지고는 문제가 생긴다!
(증명)
3. 사차방정식
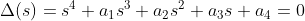
인 경우에는
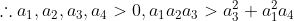
이다.
사실, 위에서 계속 근과 계수의 관계를 이용하였지만, 원래 복소수함수의 성질을 이용해서 이를 증명한다. (Routh-Hurwitz Theorem)
4. 일반적으로는,
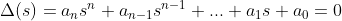
(Notation의 편의를 위해 a_n의 순서를 바꾸었다.)
다음과 같은 Table을 만든다. (빈 공간은 0으로 채운다.)
| a_n | a_(n-2) | a_(n-4) | ... | |
| a_(n-1) | a_(n-3) | a_(n-5) | ... | |
| b_1 | b_2 | b_3 | ... | |
| c_1 | c_2 | c_3 | ... | |
| ... | ... | ... | ... |
이 때,

즉,
계산할 자리의 분모는 -> 내 위의 열의 맨 앞자리
계산할 자리의 분자는 -> 내 위의 두 개의 열 맨 앞자리 + 내 위의 두 개의 열, 내 자리의 다음 행
-> 위의 테이블에선 c_2를 계산하는 방법!
이렇게 계산된 것을 가지고
-> 맨 앞의 행만 보자!!!
-> 부호 바뀐 횟수가 LHP에 없는(RHP+Imaginary axis) 해의 개수이다!
예시)
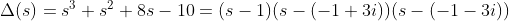
| 1 | 8 | 0 | |||
| 1 | -10 | 0 | |||
| 18 | 0 | 0 | |||
| -10 | 0 | ||||
| 0(END) | |||||
여기서 18 -> -10으로 부호 한번만 바뀌었으므로, LHP에 없는 해의 개수가 1개이다!(s=1)
여기까지, LTI 시스템의 안정성에 대한 개략적인 내용들만 보았다.
여러 내용들을 보았지만, 결국엔
-> POLE이 LHP에 있다, 없다가 안정성을 파악하는 가장 Simple한 방법!
다음시간에는 위에 잠깐 언급한 Lyapunov 안정성에 대해서 설명한다!
'제어이론 > 선형시스템 -> LTI System' 카테고리의 다른 글
| (선형시스템) 4-1. Response의 성능 in Time-Domain (0) | 2023.04.10 |
|---|---|
| (선형시스템) 3-2. Lyapunov Stability in LTI System (0) | 2023.04.09 |
| (선형시스템) 2-2. 마음대로 잡아도 되는 State-Variable (Equivalent System of LTI) (0) | 2023.04.06 |
| (선형시스템) 2-1. MIMO LTI System의 해 (0) | 2023.04.05 |
| (선형시스템) 1-3. 전달함수와 Pole, Zero (Transfer Function, Pole, Zero) (0) | 2023.04.05 |