이번에는 LTI 시스템의 전달함수만 따로 떼어서, 조금 더 살펴보도록 하자.
(Transfer function and Impulse)
앞에서 본 바와 같이, 라플라스 변환을 이용하면

그러므로, 예를 들어서 시스템에 뭐 망치로 갖다가 때린다던지 하는 Impulse를 주면, 시스템 고유의 Response가 나온다는 것을 알 수 있다!
또한, 여기서 더 나아가서 대부분의 물리량이 애초에 "유리수"로 주어지므로, (예를 들어서, 질량이 (pi) kg인 경우는 거의 없을테니)
대부분의 Transfer Functions는 다음과 같은 (유리수로 이루어진 다항함수의 분수꼴)로 나온다... 즉,
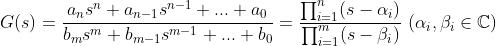
이 때,
n>=m : Improper Transfer function이라고 한다.
n<m : Proper Transfer Function이라고 한다.
사실, 우리가 원하는 시스템(Transfer Function)은 아마도 Proper Transfer Function일 것이다. (물론, 아닌 경우도 있지만)
왜냐하면,
s가 무한대로 가면(즉, 고주파수) -> Improper의 경우 무한대로 발산... -> Response가 발산... -> 시스템 불안정
이기 때문이다.
이를 해결하기 위해서 제어기(Controller)를 설계해서 시스템에 붙이는 게 우리의 목표!
(Pole and Zero)
위의 Transfer function에서,
- G(s)=0으로 만들어주는 s (즉, 분자부분의 해) (즉, alpha_i)를 Zero
- 분모부분의 해 (즉, beta_i)를 Pole이라고 한다.
(단, 이 경우 G(s)가 기약분수꼴(즉, 분자와 분모에 공통된 해를 가지지 않는다)(coprime)이어야 한다.)
이 Pole과 Zero는 시스템의 안정성(Stability)와 아주 밀접한 연관이 있다!!! -> 우리가 볼 메인 테마이기도 하다!!!
1. Pole
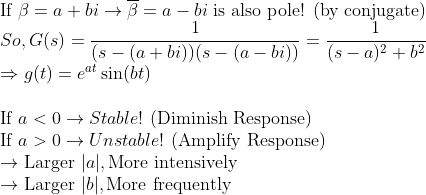
-> 즉, Pole에 따라서 시스템의 안정성(심지어 진동하는 것도)이 결정된다!
-> 다음 그림들은 Pole의 위치에 따른 Response를 대략적으로 그려본 것이다!



2. Zero
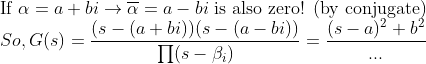
-> 즉, Zero에 해당하는 반응이 0이 나오게 되는데, 이 zero를 이용해서 안 좋은 pole(unstable하게 만드는 pole)을 상쇄시킬 수 있다.
앞 시간에 붙여놓아도 상관없을 내용이지만, 중요하기 때문에 일부러 따로 빼놓았다!!!
'제어이론 > 선형시스템 -> LTI System' 카테고리의 다른 글
| (선형시스템) 2-2. 마음대로 잡아도 되는 State-Variable (Equivalent System of LTI) (0) | 2023.04.06 |
|---|---|
| (선형시스템) 2-1. MIMO LTI System의 해 (0) | 2023.04.05 |
| (선형시스템) 1-2. LTI 시스템은 어떻게 수식으로 쓰는가? (State-Space Equation of LTI System) (0) | 2023.04.05 |
| (선형시스템) 1-1. 뭐하는 카테고리입니까? (What is Linear System?) (0) | 2023.04.05 |
| (선형시스템) 선형시스템 개요 (0) | 2023.04.05 |



