1-2에서는 SISO LTI System을 어떻게 수식으로 표현하는지 알아보았었는데, 이번엔 MIMO인 경우로 확장을 해서 보도록 하자.
여기선 라플라스 변환을 안 쓰고, 직접 구할 것인데, 이를 위해선 지수에 "행렬"이 들어간 것의 의미를 알 필요가 있는데, 사실 별거 아니고
(Exponential with Matrix)

즉, Diagonal Decomposition으로 다 쪼갠 후에 exponential 함수 태운 것이라고 생각하면 된다.
(단, Eigenvalue가 중복인 경우에 Jordan Form을 생각해야 한다.)

(즉, 중복인 Eigenvalue의 위에 1이 붙는다.)
중복인 경우만 잠시 살펴본다면

임을 알 수 있으므로,

즉, 멀어질수록 자리가 하나씩 밀렸을 뿐이지 무한합이면 exponential로 나타낼 수 있다...
그런데, 우리가 아래에서 쓸 내용은 저 Eigenvalue에 t가 붙어있다. 이 경우에는 살짝 바꿔서
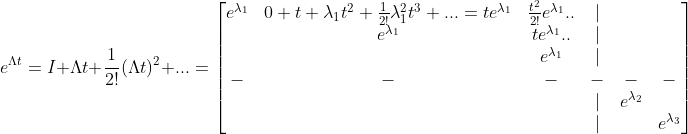
이런 식으로 쓸 수 있다.
(GIVEN SYSTEM -> MIMO LTI)
여기서 진짜로 x, y를 그대로 구해보자!

선형미분방정식 푸는 것처럼 접근을 해보면,
1. Zero-input(Homogeneous Solution)

2. With Input (Special Solutuion)
저 미방을 만족하는 특수해가 무엇일지 생각해보자....
일단, 위에서 푼 Zero-input의 해를 이용해보면

이렇게 Convolution 형태로 나오는 것을 확인할 수 있다.
이렇게 만든 저 x가 진짜 해인지 확인해보자.
1. Initial Condition 만족? -> t=0 넣어보면 만족!
2. 구한 저 x를 직접 넣어보자!

그러므로 우리가 볼 수 있는 Output y는

이라고 할 수 있다!
그리고 여기서 라플라스 변환을 쓴다면, 우리가 앞에서 했던 내용과 일치함을 알 수 있다!

여기까지는 LTI 시스템에 관한 것이고, LTV(Time-Varying) 시스템의 경우에는 Advanced 섹션에서 나중에 살펴볼 것이다!
'제어이론 > 선형시스템 -> LTI System' 카테고리의 다른 글
| (선형시스템) 3-1. LTI system의 안정성 (Stability of LTI System) (0) | 2023.04.07 |
|---|---|
| (선형시스템) 2-2. 마음대로 잡아도 되는 State-Variable (Equivalent System of LTI) (0) | 2023.04.06 |
| (선형시스템) 1-3. 전달함수와 Pole, Zero (Transfer Function, Pole, Zero) (0) | 2023.04.05 |
| (선형시스템) 1-2. LTI 시스템은 어떻게 수식으로 쓰는가? (State-Space Equation of LTI System) (0) | 2023.04.05 |
| (선형시스템) 1-1. 뭐하는 카테고리입니까? (What is Linear System?) (0) | 2023.04.05 |



