지난 시간엔 시스템에 대한 간략한 내용과, 시스템의 분류를 보았다. 그리고, LTI 시스템에 대해서 알아본다고 하였다.
LTI 시스템에 들어가기 전에, State-Variable(상태변수)에 대한 내용을 보자.
(State Variable)(상태변수)
-> 시스템에 관여하는 변수라고 할 수 있다.
ex) Mass-Spring-Damper System
(여기서 x는 x(t)로 위치를 말한다.)

사실, 여기서 State-Variable은 정해주는 사람 마음이긴 하다...
(y=x'-x로 잡는다고 해도, 아무 문제는 없다. 다만 행렬이 너무 더러워져서 문제...)
그러나, 정말로 아무렇게나 잡으면, 행렬의 특성상 너무 과다하거나, 불충분한 정보로 시스템을 제대로 표현할 수 없다.
대부분 저렇게 미분방정식 형태로 나오기 때문에, 위에서 한 방법대로, 미분값들을 각각의 변수로 잡아서 표현하는 경우가 많다!
Mass-Spring-Damper 시스템(행렬)은 시간 t에 따라서 변하지 않기에 Time-Invariant 시스템이다!
(NOTE)
센서값으로, 저 State Variable 모두를 다 보지 않을 수도 있다! -> Observability에 관한 내용
그러나, 아직 Input(외부의 힘)을 넣지는 않았다. 그리고, 우리가 센서값으로 재는 것은 오로지 위치 x라고 하자. 이를 고려하면
(State-Space Equation)
ex) Mass-Spring-Damper System

여기서 u(t)는 입력값(Input)을 말한다. 또한, vector y는 우리가 관측하는 값들을 모아놓은 것을 말한다.
이렇게 상태변수로 표현된 식을 State-Space Equation이라고 한다.
자, 그러면 이제 선형(Linear)에 대한 이야기를 해보자.
선형(Linear)에 대한 개념은 선형대수나 미분방정식에서 이미 다들 보았겠지만
-> 시스템을 일종의 함수나 mapping으로 본다면
-> 덧셈과 상수배에 대해서 다음 성질을 만족해야 한다!

그리고, 이러한 선형 mapping(시스템)은 행렬로 표현되어야 한다는 것을 알고 있으므로(선형대수 참고!)
결국, 위에서 나온 Mass-Spring-Damper System이 행렬로 표현되므로, 저 시스템은 선형이다!
(NOTE)
"선형"이라는 개념이 아주 중요한데,
-> (어떤 Input u에 대한 Response) = (Response for zero-input (u=0)) + (Response for input u)
-> 이 때, zero-input에 대한 반응이라는 것은 결국에 시스템 자체의 성질을 말한다!
ex) 선형미방에서 상수항이 추가되었을 때 어떻게 풀었었냐면...
-> (일반해) = (상수항=0인 경우의 해) + (상수항 추가되었을 때의 특수해) 였다는 것을 기억하자!
또한, Time Invariant(시간에 불변)이므로, 저 행렬들이 시간(t)에 의존하면 안된다! (즉, A=A(t)가 아니다!)
그러므로, 위에 나온 Mass-Spring-Damper System의 경우 LTI 시스템이다!
(LTI System) (Linear Time Invariant System)
선형이고, 시간에 따라 바뀌지 않는 시스템! -> 시간에 의존하지 않는 행렬로 표현!
위에서 LTI 시스템이 일종의 선형미분방정식(시간에 의존하지 않는) 형태로 주어지는데, 그러면 시스템마다 성질을 어떻게 파악해야 할까???
-> Input을 임의로 넣고, output을 분석해서 시스템을 파악해보자!
-> 특히, Impulse Input이 중요!
(미분방정식을 보면 아마 알겠지만, 이 Impulse input이 위에서 말한 zero-input response(시스템의 성질)를 그냥 준다...)
(Impulse)

즉, t_0초부터 Delta초까지의 적분값이 1인 상수함수를 Pulse라고 하는데, 이 Delta를 0으로 냅다 보내면 (존재성에 관한 얘기는 해석학의 르벡적분을 생각해보면 된다.) 그것을 Impulse라고 한다. 물론, 적분값은 그대로 1로 놓는다!
또, 우리는 임의의 Input을 Impulse의 합으로 쓸 수도 있다. (해석학 카테고리 -> Simple Function in 르벡적분 참고)
아래 그림은 일종의 예시이다...

-> 그러므로 우리의 input은 다음과 같이 쓸 수 있다.

즉, Input을 Impulse와의 Convolution으로 쓸 수 있다!!!
그러면, 이 input을 이용해서, LTI 시스템의 Response를 구해보자!
간단하게 Pulse 하나만 넣었을 때를 생각해보면...
(Response of LTI System)

그러므로 (Impulse를 넣었을 때의 Response) g와의 Convolution으로 Response를 구할 수 있다는 것을 알았다!
이 때, tau=0부터라는 것을 체크하자!
(tau<0은 애초에 말이 안된다... -> input을 넣기 전에 output이 반응한다는 것을 말하기 때문이다. -> NON-Causal System)
지금은 Single-Output(즉, g가 일변수함수)인 경우만 생각을 했는데, MIMO인 경우에도 똑같이 확장해주면 된다!
여기까지 오면 대충 감이 잡히겠지만, 라플라스 변환 혹은 푸리에 변환이 아주 유용할 것이라는 생각이 들 것이다!
왜냐면, 라플라스 변환에서 Convolution은 그냥 곱으로 변환이 되기 때문이다.
그러므로,

이 때, 시스템에 의존하는 부분을 따로 떼줄 수 있는데(G(s)) -> 이를 Transfer Function(전달함수) 라고 한다.
LTI 시스템에서 이 전달함수를 직접 구해보자!
(Transfer Function of LTI System)

(NOTE)
만약에 Time-Varying System이라면...?
-> LTI System에서 상수로 주어진 A,B,C,D가 모두 A(t),B(t),C(t),D(t)로 다 바뀌므로, laplace transform을 할 때, 문제가 생긴다!
-> 사실, 짧게 쓴다면, 처음에 A,B,C,D를 다 구할 수 있으니, 짧은 시간에는 A,B,C,D를 상수로 놓을 수도 있다.
-> 길게 쓰게 되면, 그 때마다 A,B,C,D를 바꿔주면 되는 문제.... -> 사실, 컴퓨터를 이용해서 이산적으로 계산하면 될 일
만일, Discrete-Time LTI system이라면?? -> 즉, 위에서 Delta->0으로 못 보내는 경우가 될 것이다...
-> z-transform이라는 것을 이용하면 된다! (일종의 Discreted Laplace Transform이라고 생각하면 된다.)
만약에 Nonlinear System이라면...?
-> 선형화(Linearization)을 이용한다!
(Linearization)
-> Small Perturbed Variables!

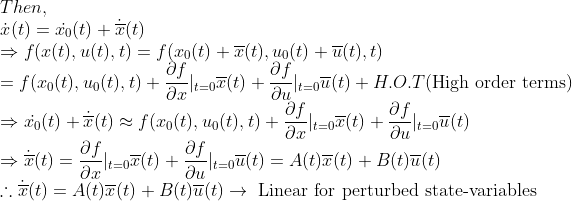
즉, Perturbed(약간만 움직였을 때) 변수에 관해서 선형으로 근사시킬 수 있다!
문제는 이 perturbed 범위가 일반적으로 꽤나 좁다는 것이 문제이다! (High 비선형성)
-> 해석학의 역함수정리와 한번 같이 보자!
뭐... 어쨌든간에, 이러한 방식을 이용한다는 것만 알자.
여기까지, 시스템을 어떻게 수식으로 옮기는지 정리하였고, 다음시간엔 Transfer Function에 대해서 약간 더 설명한다!
'제어이론 > 선형시스템 -> LTI System' 카테고리의 다른 글
| (선형시스템) 2-2. 마음대로 잡아도 되는 State-Variable (Equivalent System of LTI) (0) | 2023.04.06 |
|---|---|
| (선형시스템) 2-1. MIMO LTI System의 해 (0) | 2023.04.05 |
| (선형시스템) 1-3. 전달함수와 Pole, Zero (Transfer Function, Pole, Zero) (0) | 2023.04.05 |
| (선형시스템) 1-1. 뭐하는 카테고리입니까? (What is Linear System?) (0) | 2023.04.05 |
| (선형시스템) 선형시스템 개요 (0) | 2023.04.05 |



