(미적분학 참고링크)
(미적분학) 17-2. 드디어 마지막, 스토크스 정리 (Divergence, Curl in 3D, Stokes' Theorem): https://0418cshyun.tistory.com/39
(미적분학) 17-2. 드디어 마지막, 스토크스 정리 (Divergence, Curl in 3D, Stokes' Theorem)
지난 챕터에선 2차원 평면에서의 divergence와 rotation을 보았다. 이번엔 3차원 공간에서 알아보자. 정의는 2차원과 똑같다! (Divergence(발산)) (Curl) 보면 알겠지만 rotation은 curl의 2차원 버전이었다고 생
0418cshyun.tistory.com
이번 챕터에선 미적분학에서 보았던 Stoke's Theorem(스토크스 정리)를 "미분형식"을 이용해서 조금 더 세련되게 보려고 한다.
미적분학에서 본 스토크스 정리는

이런 느낌이었다는 것을 상기하면서 들어가자!
우리가 증명하고자 하는 스토크스 정리는 더 일반화 되어있는 형태이다!
(Stoke's Theorem)

증명을 하기 전에, 이 정리가 위에 나온 정리에 일반화된 form이라는 것을 확인해보자.
1. k=m=1 -> 미적분학의 기본정리!

2. k=m=2 -> Green's Thm(2D에서 보면) 혹은 위의 Stoke's Thm(3D에서 보면)

3. k=m=3 -> Divergence Theorem(발산정리)

여기서 나오는 dS, ds, dV에 대한 내용은 미적분학에서도 했던 내용들이지만, 뒤에서 다시 한번 또 다룰 것이다.
그러면, 본격적으로 증명을 해보자!

(증명)
먼저, psi가 k-chain일 필요가 없다! -> k-simplex면 충분하므로, simplex로 가정하고 시작한다!

이를 증명하기 위해서 경우를 나누자.
1. k=1

2. k>1

여기서 나온 tau에 대해서 더 자세히 써보자...

이를 다시 행렬표현으로 쓴다면...
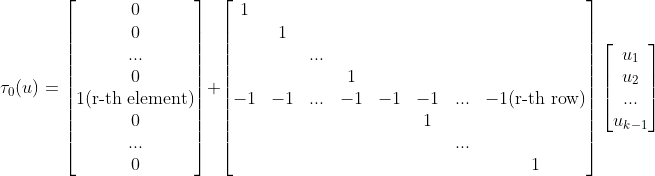
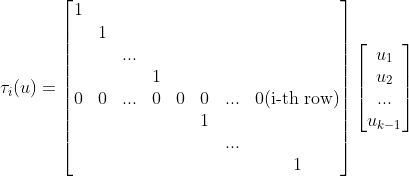
그러면, tau로 인한 determinant를 계산해보면
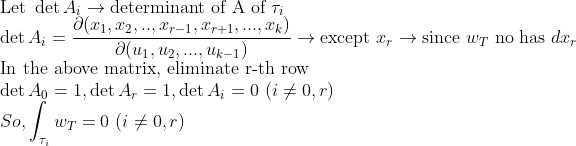
자, 그러면 이제 다시 돌아와서...
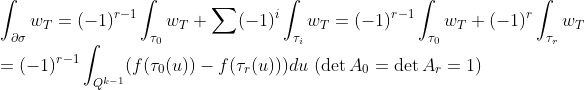
이제 반대편 쪽 항을 보면

그러므로 증명이 완료되었다.
(Simplex에서 성립하므로 Chain에서도 동일하게 성립!)
스토크스 정리를 응용하는 것은 이미 미적분학에서 본 것으로도 사실 충분하기 때문에 (어차피 일반적이라고 하지만 결국엔 2차원 3차원에서 대부분 쓰게 된다....) 의미와 응용은 미적분학에서의 내용을 참고하기 바라고, 조금 더 뒤에서 선적분과 면적분을 보면서 응용에 대해서 더 이야기 할 것이다.
스토크스 정리가 미적분학의 기본정리를 포함한다고 했는데, 미적분학에서 배울 때, 이에 관련해서 Potential Function과 Exact form 등의 내용을 배웠었는데, 그럼 이러한 방식의 스토크스 정리에서도 똑같이 적용이 될 것이다. 이에 관한 내용을 다음에 다룰 것이다



