저번 시간에는 Exact Form과 Closed Form에 대해서 다루었는데, Exact Form 자체가 Potential function의 존재성을 말해주므로, 미분형식이 Exact Form인지 아는 것이 중요했다.
그런데, Exact Form이면 Closed Form이 되므로, 이 역도 성립하는지가 궁금하다.
이 역이 바로 푸앵카레 보조정리가 된다.
(Poincare's Lemma)

즉, Convex set에서 Closed Form이 Exact Form이 된다.
더 나아가서 Convex set일 필요도 없고, 한 점에서 convex -> Star-Shape이기만 하면 된다! (in 미적분학)
이를 증명하기 위해서, 먼저, 다음 lemma를 하나 살펴보자.
(Lemma)

즉, 어떤 고정된 p에 대해서 위 조건을 만족하는 Potential Function이 존재함을 말해준다.
(증명)
n차원에서 p차원으로 끌어내려서 생각해보자.

만일 p=1이면 V는 어떤 구간이 된다..

p>1이면 똑같은 방법으로 p-1차원으로 끌어내려서 생각해보자.

그러므로 증명이 완료된다.
그러면, 본격적으로 푸앵카레 보조정리를 증명해보자.
(Proof of Poincare's Lemma)
k는 주어진 값이라는 것을 상기하자!

p=1인 경우에는 간단하게 증명할 수 있다.

p>1인 경우에는 귀납법을 이용해서 접근하자!
(주어진 p에 대해서 p-1까지 True -> p+1인 경우에 true???)

그리고, 귀납법을 쓰기 위해 w를 p-1에 들어가는 부분과 아닌 부분으로 나누어서 생각해보자!
(I_0를 p-1까지, I는 p까지)

gamma가 Y_{p-1}에 들어가므로, gamma는 exact form이다.(by 가정)
그러면, 이를 이용해서 w의 potential도 구할 수 있다!

그러므로 귀납법에 의해 증명이 끝난다.
그런데, 위에서 Convex 말고, Star-shape인 경우에도 된다고 하였었다....
어떻게 확장을 할 수 있을까?? -> Just Transformation!
(Extension of Poincare's Lemma)

즉, C2-mapping에 대해서 inverse가 잘 정의되어 있으면 Transformation을 이용해서 Convex set을 확장시킬 수 있다.
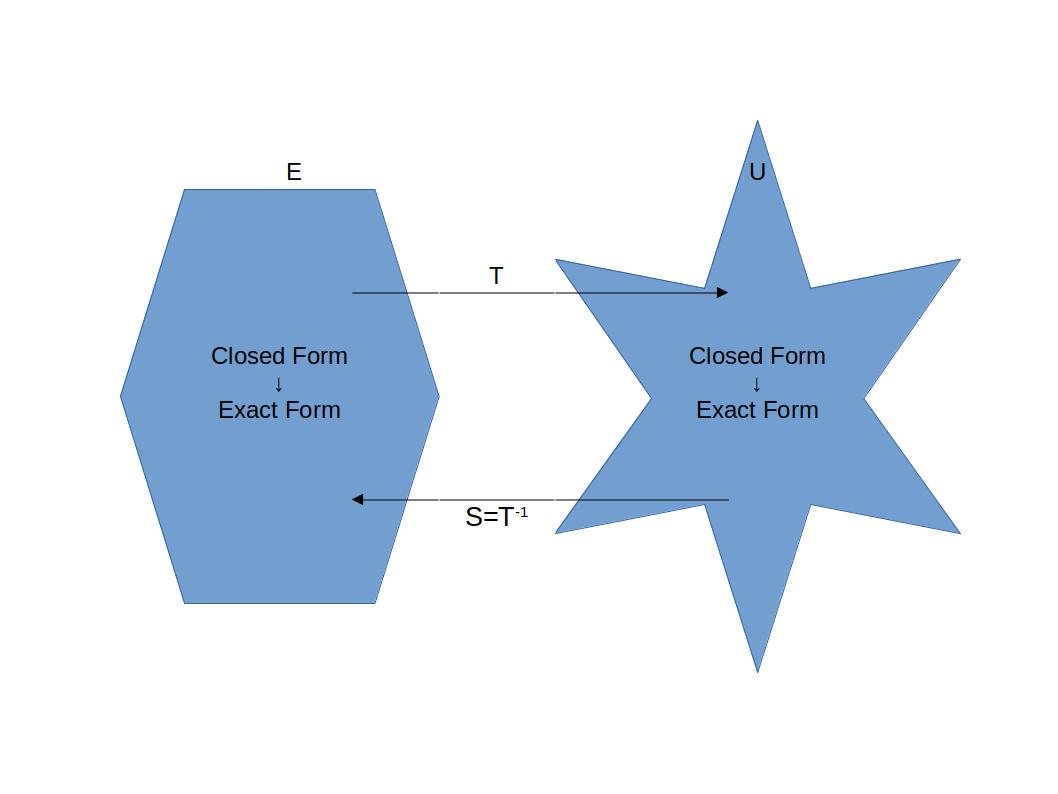
(증명)
미분형식을 Transformation 태워보내는 것을 이용하면 간단하다!
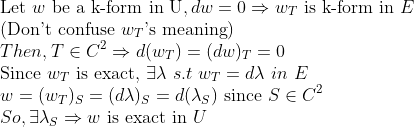
그러므로 Star-shape를 포함해서 더 일반적인 Domain에서도 Closed Form과 Exact Form의 관계를 알 수 있다!
여기까지, Poincare's Lemma를 살펴보았다.
-> (Convex set을 C2-mapping으로 보낸 Domain에서) Closed Form이면 Potential 함수가 존재한다는 것을 알 수 있었다.
미분방정식이나 여러 응용에서(전자기학이나 유체역학이나 벡터장을 이용한 거의 모든 응용) Potential 함수가 존재하면, 아주 간단하게 문제를 풀 수 있기 때문에 아주 중요한 정리가 된다. (물론, 응용할 때는 Convex인지 아닌지 거의 안 따지지만...)
다음시간에는 드디어 선적분, 면적분 -> 벡터장 etc...에 관한 "응용"적인 내용으로 들어가보자.



