이번에는 감마함수와 함께, 조금 더 들어가면 또 가끔 더 보이는, 베타함수에 대해서 알아보자.
(Beta Function)

베타함수는 적분으로 정의해도 상관없고, 감마함수를 이용해서 정의해도 상관없다.
사실, 등장빈도는 감마함수에 비해서 낮긴 하지만, 저 적분꼴이 은근히 많이 등장하므로, 딱 그냥 상식정도로 알아두자...
여기서 베타함수의 두 식이 같은 것임을 증명해보자! -> 감마함수의 성질을 이용한다.
(증명)
일단,

인 것을 가정해서 시작하자!
그러면,

이 함수 f(x)가 감마함수의 성질 3가지 모두를 만족하는 것을 보이면, f(x)가 감마함수가 되어, 위 식을 증명하는 것이다.
그럼, f(x)가 감마함수의 성질을 보이는 것을 확인하자.
1.

그러면,

2.
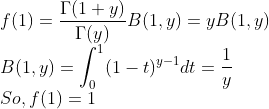
3.
먼저 log B(x,y)가 Convex임을 보인다. 이는 감마함수에서 했던것과 동일하게 하면 된다. -> 이 때, y는 그냥 고정하면 된다!

log f(x)가 convex임을 보이기 위해 a,b로 잘 쪼개준다!

그러므로 세 성질을 모두 만족하므로,

결국 베타함수도, 감마함수와 거의 동일하게 취급할 수 있다는 것을 알 수 있다.
베타함수를 이용하면, 감마함수에 대해서 더 자세히 구해볼 수도 있는데,

어떻게 보면, 곧바로 적분이 불가능해보였던

를 계산할 수 있다!
또한, 다음과 같이 응용해볼 수도 있다.

극좌표계 변환을 이용해서 풀었던 위 식도 풀 수 있다.
또한, 이를 이용해서 감마함수를 다음과 같이 쓸 수도 있다!
앞에서 배운 Gamma 함수의 lim식을 이용해보면 -> Gamma(2x)를 억지로 Gamma(x), Gamma(x+1/2)로 나누고 나머지를 생각해보자.

이 때, 나머지는 다음과 같다. (극한에서 팩토리얼 처리하는 경우 빨간색, 파란색의 경우처럼 나눠버리는 경우가 많으니 참고)

또, n=2k+1인 경우도 동일하게 접근하면 위와 같은 식을 얻을 수 있다.
그러므로,

보면 알겠지만, 사실, 결과를 알고 있는 경우에는 억지로 저 꼴을 만들어서 증명하는 것이 편리하다. (이게 결국엔, 많이 알면 어쩔 수 없이 유리한 이유...)
굳이 힘들게 억지로 막 집어넣어서 도출하는 게 나쁘다는 것은 아니지만, 효율성은 떨어진다.
여기까지, 감마함수와 베타함수에 대해서 알아보았다. 물론 더 많은 성질들이 있지만, 여기까지 하도록 하고,
다음시간에는 다변수벡터함수인 경우에 미분과 적분을 어떻게 정의하는지 들어가보자!



