지난시간에 이어서 조금 더 나아가보자!
Linear Transformation은 하나의 Mapping에 대한 것이었다면, 이 Linear Mapping들을 모아놓은 공간을 생각해보자!
(Space of linear transformation)

1. 그러면, 이 공간은 Vector Space이다. (벡터 대신 행렬을 쓴 것 밖에 없다!) 즉,

즉, 덧셈과 상수배에 대해서 닫혀있다.
2. 또한, (행렬이 아니더라도) 교환법칙이 성립하지 않는다! 간단하게 예를 들자면...

BA의 경우에는 저렇게 mapping 순서가 맞는데,
AB를 만드려니 x는 Y에서 와야하고 결과는 Z에 있는데, 이를 다시 A에 넣을 수는 없다.(Domain이 X이므로)
그러니, 일반적으로 교환법칙이 성립하지 않는다.
3. 만일, 벡터공간 X,Y가 "유한차원" 유클리드 공간이라면, (Space of linear transformation)의 각 원소마다 Norm을 설정해줄 수 있다. 즉, (Linear Transformation)의 Norm을 다음과 같이 정의한다.
(Norm of Linear Transformation)

사실, 이 경우의 Linear transformation은 행렬이라는 것을 알고 있으므로, 행렬의 Norm을 정의해준 것과 다름이 없다!
(Norm of Matrix)

여기서 하나 참고해야 할 것은 2-norm과 Frobenius Norm은 서로 다르다는 것이다! -> 선형대수학에서 더 살펴보기로!
(Note) -> (Norm of vector)

(NOTE)
(유클리드 공간 -> 각 벡터에 Norm!)
(함수공간 -> 각 함수에 Norm!)
(선형변환공간 -> 각 선형변환에 Norm!)
-> 맨 위 Linear Transformation의 Norm의 경우, 결국 2-norm을 말하고 있다! (계속 벡터의 절댓값을 2-norm으로 보고 있다!)
-> 위에서 저렇게 정의한 Norm은 실제로 Norm의 성질을 만족한다!
그러므로 다음과 같이 말할 수 있다!

자 그러면, 이렇게 정의해준 Norm으로 몇가지 성질을 더 보자!
1. (Bounded Norm)

(증명)
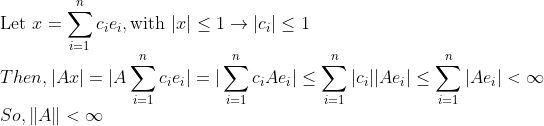
x를 각 성분별로 나눈 후에 Ax를 구해보면, 저 e_i들이 standard basis이므로, Ae_i들 각각은 분명히 R^m에 존재하고, 벡터의 norm이 infinite가 아니니, Ae_i들의 norm의 유한합은 당연히 infinite가 아니다!
그리고, Uniform Continuous는 다음과 같이 증명할 수 있다!

2.

(증명)
sup에 해당하는 범위가 더 커진다면, sup 값도 더 커질 수 있음을 생각하자!
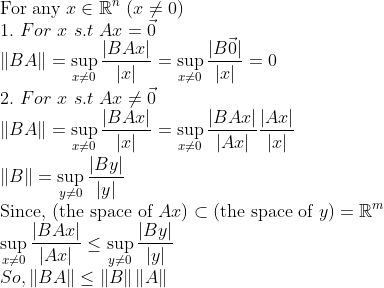
여기까진 norm 자체에 대한 성질이고, 이제 조금 더 깊게 들어가기 위해서 앞에서 본 Invertible(역행렬)과 norm을 이어보자!
(Norm and Invertible Transformation)

역행렬이 존재하는 행렬의 집합이 Open set이라는 것을 알아두자!
(증명)
1번의 빨간부분은 꼭 알고 넘어가자!
1.
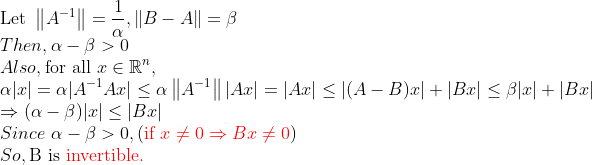
빨간부분이 중요하다! -> Invertible과 (Bx=0 -> x=0) 은 서로 "동치"이다!
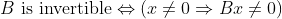
다음과 같이 생각해보자.
a. ->
Invertible을 가정해보자.
Bx=0의 해를 구한다고 하자.... -> 만일 역행렬이 있으면, 양변에 역행렬을 곱하면 되니, 해는 x=0 밖에 안 나올 것이다.
b. <-
(귀류법을 이용하자) 만약에 Invertible이 아니라고 가정해보자.
그러면, (미적분학에서 본 것처럼) B의 행(또는 열)벡터들이 linear dependent이다.
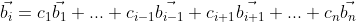
이 때, 어떤 x에 대해서 Bx=0이라고 하자. 그렇다면
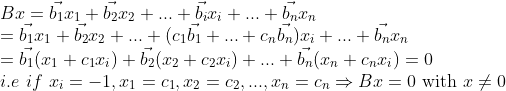
모순이 생기므로, Invertible이어야 한다!
2.
1번에 의해서
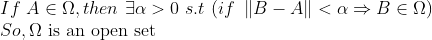
또한, 연속성을 보이기 위해서 1번을 이용하면
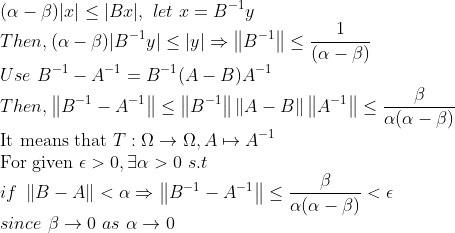
즉, 주어진 epsilon에 대해서, alpha, beta를 충분히 작게 잡으면 저 T가 연속임을 보일 수 있다!
자, 여기까지 한 내용을 다 정리하자면
1. 유클리드 공간 사이의 선형변환들의 공간의 원소는 일단 "행렬"로 나온다! 즉, (유클리드 공간 사이의) 선형변환은 행렬이다!
-> (미적분학 꼭 참고!)
2. 만일, Invertible한 원소들로만 모인 공간을 Omega라고 한다면,
-> Omega는 open set
-> Omega의 원소 A는 행렬일텐데, A의 각 원소들은 연속함수이다! (행렬의 각 자리에 연속함수가 들어간다!)
여기까지 다변수벡터함수에서 쓰일 선형대수에 관한 내용들을 간략하게 정리해보았다. 다음 챕터부턴 다변수 벡터함수의 미분에 관한 내용으로 들어가보자!



