이번챕터에서는 역함수의 미분에 대해서 알아보도록 한다.
다들 이미 알고 있겠지만 일변수함수(SISO)에서는 아무생각없이 다음처럼 계산했었다.
(어떤 변수로 정리하는지 꼭 확인하자! x->y)
혹시나 미분을 뉴턴식으로 표기하는 사람이 있다면, 여기서만이라도 꼭 라이프니츠식으로 바꿔서 생각하자. 정말로 헷갈린다!
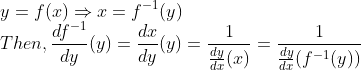
이런 식으로 계산했었다...
예를 들어서
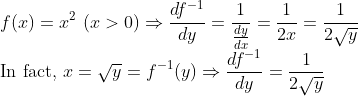
그러니까 위의 내용은 결국엔
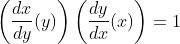
이라는 것이고, (dx/dy는 결국 x를 y로 미분하는 거니 (일차적으론) y에 대한 식으로 나올 것이다. dy/dx의 경우도 마찬가지)
이를 증명하는 거야
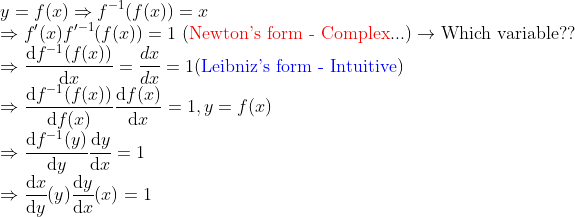
이런 식으로 했었는데, 수식 쓰는거야 간단하지만, 여기엔 문제점이 있다.
역함수가 있긴 하니?
주어진 x, 혹은 domain에 대해서 역함수가 존재해야 한다는 것이다....
일변수라면, 1 to 1 -> 단조함수로 역함수의 존재조건이 정리가 되겠지만 다변수벡터함수라면 어떻게 될지 감이 오는가??
-> 이를 고려해서 역함수 정리(Inverse Function Theorem)가 등장하게 된다!
역함수 정리를 들어가기 전에 Contraction(축소) 개념을 알아야 한다.
(Contraction)
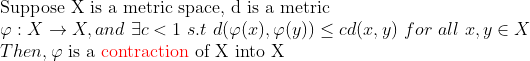
그러니까, 저 phi함수를 태우면, 원소 사이의 거리가 원래보다 축소된다!!!
-> 만약에 phi함수를 무한번 태우면...? -> 거의 한 point로? -> Complete Space라면 가능하다!
(Complete Space가 아니면, 한 point를 그 space에서 고를 수 없을 것... -> 유리수 안에서 유리수 수열의 수렴성을 보장 못한다는 것을 생각하자!)
(Existence and Uniqueness of Contraction)
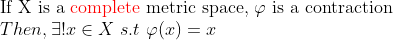
즉, Complete Metric Space에서 Contraction이 몰리는 point가 존재하고, 그 point는 유일하다!
그리고 그 점을 Fixed Point(고정점)라고 한다!
(증명)
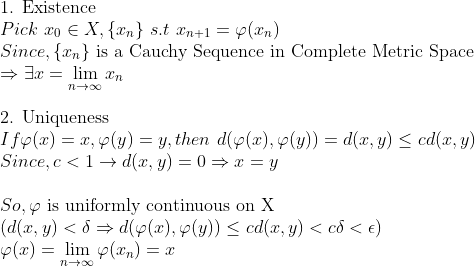
Complete Metric Space임을 이용하면 쉽게 보일 수 있다!
또한, 역함수 정리를 들어가기 전에, 미분에 관해서 다음과 같이 생각할 수 있다.
미분의 정의에서
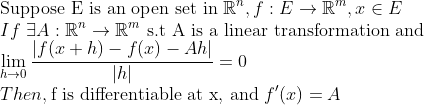
1. f는 x 뿐만이 아니라, x 주변의 Open set인 E에서 정의되어 있어야 한다.
2. x 주변의 Open set인 E에서 위 식을 만족하는 Linear Transformation A가 존재해야 한다...
--> 즉, f'(x)가 Linear인 영역이 E라고 할 수 있다! / E를 벗어난다면 f'(x)는 Non-linear일 수 있다!
특히, E를 x 주변의 어느 Open set -> Locally Open set(Neighborhood)라고 할 수 있다!
그렇다면, 이제 역함수 정리를 들어가보자!
(Inverse Function Theorem)
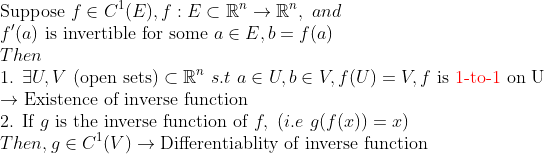
즉, 역함수정리의 목적은 역함수의 미분값을 계산하는 것이 아니라
-> 실제로 역함수가 존재하는지, 그리고 미분가능한지를 따지는 것이다!
-> 결과적으로, f'(x)가 Linear한 영역(Locally Open Set)에선 역함수정리를 쓸 수 있다!!!
증명이 길기 때문에, 여기서 역함수 정리의 의미를 살펴보자...
가정 -> E에서 f'(x)가 Invertible... -> 즉, f'(x)가 Linear Transformation으로 나오는 영역에서!
그러면..
1번의 의미 -> f가 1-to-1이고, onto (일대일 대응!)인 영역(U,V)을 잡을 수 있으니 -> 적어도 이 영역에선 1대1 대응이므로, 역함수가 존재한다!
2번의 의미 -> 그러한 역함수를 g라고 하면, g는 미분가능하고, 그 결과값도 연속이다! -> 맨 위의 공식을 그대로 이용할 수 있다!
(증명)
증명이 꽤 기니, 정리하면서 간다!
1. 존재성
f는 a에서 미분가능하니 당연히 연속이므로 다음과 같이 생각할 수 있다.
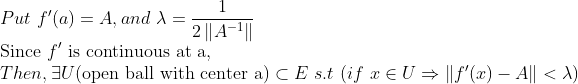
또, R^n에 있는 각각의 y에 대해서 함수 phi를 다음과 같이 정의하자!(마치 역함수처럼...)
각 phi_y에선 y는 주어진 값이므로, 그냥 상수로 처리하자!
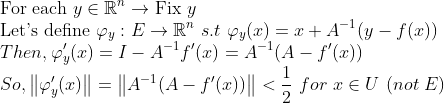
MVT와 contraction을 이용하면 다음과 같이 정리할 수 있다.
정리하면, y가 주어지면 각 y마다 contraction을 구할 수 있고, 거기에 따른 unique한 x를 구할 수 있다.
이 x가 fixed point이면, phi에 넣게 되면, y=f(x)를 얻을 수 있으므로, f는 1-to-1이다!
즉,
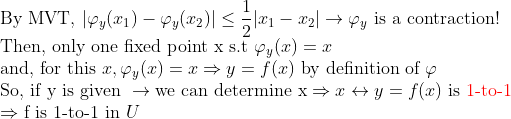
그럼 이제 f(U)=V를 만들어 V가 open set인지 따져보자!

그러므로 이 위에서 했던 것처럼 생각하면
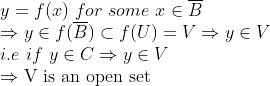
그러므로 1번 증명이 끝난다. (a는 U의 중심이고, 그러므로 a가 U의 원소, b는 V의 원소가 된다.)
2. 미분가능성
위의 U,V에서 각각 원소를 뽑아서 저 Contraction에 넣어보자!
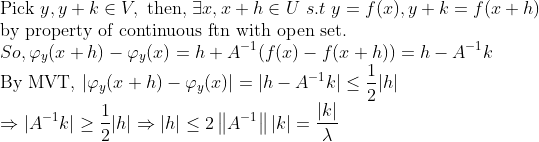
1번에서 역함수가 있다는 것을 보였다. -> g!
그러면, 이 역함수의 미분값은 존재하는가? (즉, 역함수가 미분가능한가?)
일단 f'(x)의 역함수가 존재하는지 보자...(f'(a)가 아니라!) -> 15-2에서 본 Omega(set of invertible linear transformations)의 성질을 이용하자!
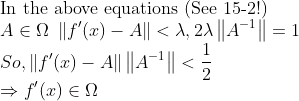
그러므로, f'(x)는 inverse가 존재한다. 그럼, 존재성을 알았으니, 미분가능한지 알아보자!
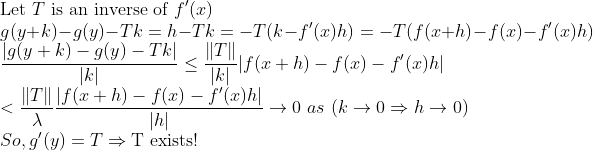
저 T가 존재하므로, 미분가능하다!
미분가능을 넘어서 이 결과값이 연속이라는 것은 우리가 선형대수에서 했던, Invertible linear transformation이 연속함수라는 것을 이용하자! -> 15-2에서 본 Omega(set of invertible linear transformations)의 성질을 이용하자!

그러므로 이를 이용해서 다음과 같은 결론을 얻어낼 수 있다.
(Corollary)
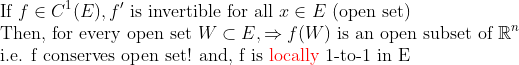
즉, f가 위 조건을 만족한다면,
1. f가 Open set을 보존한다... (연속성질에서 f의 역함수가 open set을 보존했던것을 생각해보자...)
2. f가 locally 1-to-1이다!
결론적으로, 역함수의 존재성은 Locally(부분적으로)만 증명이 가능하고, Globally하게는 이야기하기 어렵다....
별거 아닌 정리같이 보이지만, 이 역함수정리는
일반적인 방정식의 해를 구하는 문제
로 귀결이 되는데, 심플하게 예를 들어서
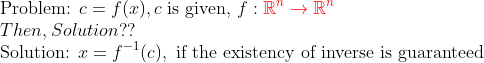
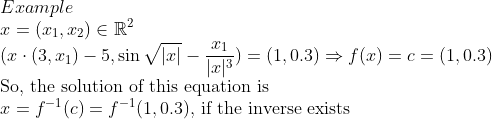
즉, Inverse의 존재성이 입증이 된다면, 그냥 Inverse 때려버리면, 방정식의 해가 튀어나온다!
물론, 여기엔 여러 장벽들이 곳곳에 숨어 있긴 하다...
1. 역함수 정리의 f는 R^n -> R^n 을 만족해야 한다.
즉, 변수가 n개, 식이 n개여야 한다. -> 더 일반적인 방정식의 경우?? (변수 n개, 식이 m개) -> 뒤의 음함수 정리(Implicit Function Theorem)을 보자!
2. 저 Solution 위치에서 역함수의 존재성을 말할 수 있는가??? -> 우리가 배웠듯이 Locally(예시에서는 x,y가 주어지고, 그 위치에서만) 역함수가 존재하는지 안다... -> 즉, Globally(모든 x,y에 대해서) 저 f의 역함수가 존재하는지 모른다....
어떻게 보면 방정식을 푸는데에 가장 파워풀한 Tool이 바로 역함수정리(Inverse Function Theorem)이지만, 저 위의 두 장벽 때문에 실속을 따지기가 굉장히 어려워진다....
물론, 미분방정식의 경우도(다변수가 된다면) 저런식으로 문제가 생길것이다....
다음챕터에서는 음함수정리에 대해서 알아보자!



