지난 챕터에선, 역함수 정리에 대해서 살펴봤었는데, 끝에 살짝 언급한 것과 같이,
역함수의 존재성이 일반적인 방정식의 해의 존재성과 일치한다는 것을 보았었다. 여기에 대해서 더 자세히 보자...
(일반적인 방정식의 해의 존재성)
어떤 방정식이 주어졌다고 하자....
그러면 그 방정식이 무엇이든 간에 한 쪽으로 몰아서 작성할 수 있다.
예를 들어서,

이렇게 복잡한 방정식도, 결국에 한 쪽으로 몰면 위처럼 정리가 된다.
그런데, 만일, f가 linear(행렬)라면... -> "선형" 연립방정식의 해를 구한다고 생각을 해보자... -> 결국 선형대수에서 하는 것!

1. 변수의 개수= 식의 개수이면, (해가 있다면) 유일한 해를 가진다는 것을 알 수 있다! (역함수(역행렬)의 존재성!)
ex) 3x+y=4, x+y=2 -> x=1, y=1 (unique solution)
2. 변수의 개수 > 식의 개수인 경우, (해가 있다면) 해가 유일하지 않을 수 있다는 것을 알 수 있다! (부정형 방정식)
ex) 3x+y=4를 만족하는 (x,y)는 매우 많다... -> 그래프 위의 모든 점이 Solution
그런데, 우리가 여기서 남는 변수만큼을 지정해준다면 x는 Uniquely 결정된다!
ex) 위에서 y=1이라고 하자... -> 그러면 x=1은 Unique solution이 된다.
3. 변수의 개수 < 식의 개수인 경우에는..? (선형대수의 pseudo inverse -> 이건 정확한 해를 구한다기 보다는, 주어진 방정식을 가장 잘 만족하는(???) pseudo solution을 구하는 것이다!) -> 이 얘기는 선형대수에서 알아보자!
그런데, 여기선 주어진 f가 선형은 아니다! 그러나 우리가 볼 세가지 정리는 저 f를 적어도 Locally 선형으로 볼 수 있게 해준다.
이번에도 주어진 식의 개수와 변수의 개수를 따져보자...
1. 변수개수 = 식 개수
-> 역함수 정리(Inverse Function Theorem)!
2. 변수개수 > 식 개수
-> 음함수 정리(Implicit Function Theorem)!
3. 그냥 일반적인 경우....
-> Rank Theorem!
나중에 결론적으로 나오는 내용이지만, 위 세 정리가 공통적으로 말해주는 바는
주어진 어떤 점 a에 대해서, f'(a)가 Invertible이면 (혹은 부분적으로...)
-> f'(a)가 선형인 범위를 a 근방에서 Locally 잡을 수 있다!(역함수 정리, 음함수 정리, Rank Thm의 의미)
-> 그러면, f를 Locally 선형으로 볼 수 있다! (위의 "선형"연립방정식처럼 생각할 수 있다.)
(f(x+a)=f(a)+f'(a)x)
-> 그 점에서 역함수(역행렬)를 잡아버릴 수 있다!
-> Locally Solution을 구할 수 있다!
본격적으로 음함수 정리에 들어가기 전에, 잠깐 Notation을 보고 들어가자.

행을 n개와 m개로 쪼갰다고 생각하면 된다!
그럼, 음함수 정리의 문제 상황을 한번 정리해보자.
위에서 본 것과 같이, 이번엔 변수 개수(n+m) > 식의 개수(n) 인 상황이다.
그런데, 해를 정확히 구하기 위해선 남는 변수들을 지정해줘야 한다. -> 선형연립방정식 case의 2번 상황!
그러므로, 우리는 여기서 x를 "우리가 구할 변수", y를 "지정해 줄 변수"라고 할 수 있다.

그럼 저 방정식의 해는 어떤 식으로 써질까?

즉, 위의 g(y)가 방정식의 Solution이 될 것이다. -> y가 정해지면 x가 정해지는 것을 알 수 있다!!!
이 g(y)의 존재성을 논하는 것이 바로 음함수정리(Implicit Function Theorem)이다!
(Implicit Function Theorem)(음함수 정리)

천천히 읽어보면, 결국 역함수정리에서 변수 개수만 커진 느낌이라는 것을 알 것이다.
(증명)
1. 존재성
차원을 확장해서 생각해보자... -> 역함수정리를 쓰기 위해서, (n+m) -> m인 함수 f 말고, (n+m) -> (n+m)인 함수 F를 정의해보자!

F'(a,b)가 invertible인 것은 determinant 말고도 다음과 같이 보일 수도 있다.

자, 그럼 F에 대해서 역함수 정리를 이용할 수 있다. 그리고, 우리가 원하는 만큼 차원을 다시 줄여보자! 그러면 1번 증명이 끝난다!
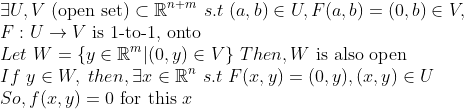
또한, f(x,y)=0을 만족하는 x가 unique함을 보이자!
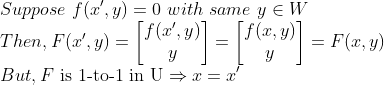
2. 미분가능성
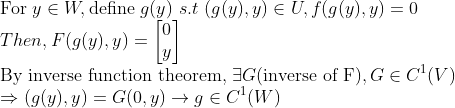
g'(b)를 구해보자!
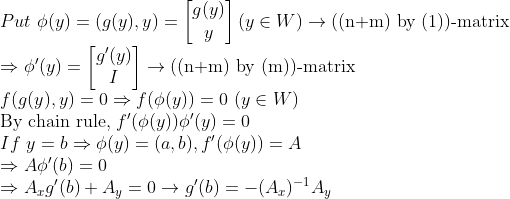
되게 복잡해보이지만, 결국엔 역함수 정리와 별반 다를 바가 없다!!
변수 개수 > 식의 개수 인 경우에
1. 남는 변수들을 다 정하고, 구할 변수에 관한 식들이 Full Rank이면(즉, Invertible) 구하는 변수가 Unique하게 정해진다!!
또한, "구할 변수에 관한 식들이 Full Rank이면(즉, Invertible)" 라는 말은
2. 거기에 해당하는 행렬이 역행렬이 존재하고, 그 역행렬의 미분도 가능하다! -> 역행렬의 미분가능성!
자 여기에선, 주어진 식이 모두 의미가 있었다. 즉, Full-Rank였다.
그러나, 우리가 연립방정식이나 선형대수에서 이미 알고 있듯이, 같은 정보를 가진 식들도 등장할 수 있다. 혹은 식이 서로 상충되는 경우도 있을 것이다. (Not Full Rank...)
예를 들어서, 3x+4y=0 .... 6x+8y=4 -> No....(서로 상충됨...)
-> 이러한 경우를 고려해서 다음 챕터에선 Rank Theorem에 대해 살펴보자!!!



