이번시간에는 푸리에 급수를 가지고 어떻게 응용하는지 잠깐 예시를 볼 것이다!
1. 수학적인 Application
a. 급수의 계산
b. 편미분방정식의 응용 -> 나중에 미분방정식 카테고리에서 다룰 예정!
2. 공학적인 Application
a. Fourier Transform (Frequency Domain) -> 센서값 필터링 (Low-Pass Filter(LPF), High-Pass Filter(HPF))
b. Discrete Fourier-Transform(DFT), Fast Fourier-Transform(FFT)
이 외에도 여러가지 쓰임새가 있겠지만, 일단 이 정도로 보도록 한다.
1. 급수의 계산

위와 같은 급수가 수렴한다는 것은 이미 다들 알고 있을 것이다.
그런데, 이 값을 계산하라고 하면, 사실 막막할 것이다.... (수렴하는건 아는데, 얼마지...?)
이 때, 앞에서 배운 Parseval's Theorem이 이 급수를 계산하는데 아주 큰 역할을 한다!!!
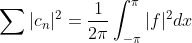
저 c_n=1/n이 되는 f만 찾으면 되는 것이다!
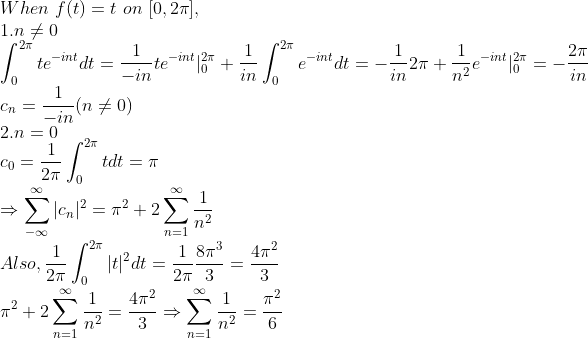
이를 이용해서 다양한 형태의 급수를 계산할 수 있다! (즉, f만 잘 잡으면 그에 맞는 급수를 계산할 수 있다.)
2. 편미분방정식에서의 응용
-> 이건 나중에 미분방정식 카테고리에서 따로 다루겠다!
-> 미분해도 자기 자신을 가지고 있는 것이 아주 큰 장점이 된다!
3. Frequency Domain
푸리에 급수는 함수 f(x)를 sin, cos 으로 나타내는 것이라고 할 수 있었다.
그런데, 변수 x를 시간 t라고 생각한다면 물리적으로 이 sin nt, cos nt로 변환하는 것은 다음과 같이 생각할 수 있다.
진동하는 시스템(혹은, 파동)에서 항상

각속도는 결국에 주파수(Frequency)와 동일하므로

즉, 위에서의 각각의 a_n,b_n -> Fourier Coefficient c_n은 각 주파수별로 f가 가진 "세기"라고 할 수 있다!
그래서, 다음과 같은 변환(mapping)을 Fourier Transform(푸리에 변환)이라고 한다!
(NOTE) 함수를 받아서 함수를 결과값으로 뱉는다!

또한, 이 Transform의 역변환도 또 정의할 수 있을 것이다. (Fourier Inverse Transform)(푸리에 역변환)
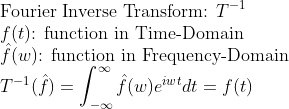
이를 이용하면 Low-Pass Filter, High-Pass Filter를 만들수도 있다.
(물론, 회로적으로 만드는 것 말고, 굳이 따지자면 후처리...?)
예를 들어서 노이즈캔슬링을 한다고 하자.
지지직대는 잡음은 대부분 High-Frequency를 가지고 있다. -> 이를 제거하려면 high frequency를 일부러 지우고, Low frequency영역만 보존하면 된다. (Low Pass Filter)
그리고 사람이 거슬리는 진동음(쿵쿵대는 소리, 버스 소음 etc....)은 대부분 Low-Frequency를 가지고 있다. -> 이 경우도 위와 같이 제거하면 된다. (High Pass Filter)
---> 즉, 본인이 원하는 영역만 딱 골라서 주파수영역을 변경하면 된다! (물론, 원하는 영역을 정하는 것이 쉬운 일은 아니다.)
이는 Fourier Transform을 이용하면 된다!
ex)
소리에서의 함수 f(t)를 받는다.(마이크 등 센서) -> 푸리에 변환! -> 주파수 영역에서 원하는 영역만 남기고 나머지는 0으로 지우거나 변경한다. -> 푸리에 역변환! -> 스피커로 내보낸다! -> 노이즈 캔슬링....
4. Discrete Fourier Transform, Fast Fourier Transform
a. Discrete Fourier Transform(DFT)
위에서 본 푸리에 변환은 변환된 함수가 연속적인 함수였다. (여기서의 연속은 수학적인 연속함수가 아니라 Discrete(이산적)을 말한다.)
예를 들어서, 우리가 배웠던 푸리에 급수에선, 주파수가 1.5, 3.55 이런 식은 불가능했다....
그러나, 위에서 소개한 푸리에 변환에서는 주파수가 굳이 Integer여야 한다는 가정은 없었다! -> 연속적인 주파수 Domain!
이를 컴퓨터에서 계산한다고 했을 때, 컴퓨터 자체가 이산적인 계산에 최적화되어있기 때문에, 위처럼 푸리에 변환을 쓰긴 어려울 수도 있다.
그러므로, 우리가 푸리에 급수에서 했던 것처럼, 이산적으로 푸리에 변환을 하는 것이 바로 Discrete Fourier Transform이다!
(물론, 컴퓨터에서 급수를 무한대까지 더하는 일은 없으므로, 원래 함수에서 약간에 손실이 있을 수 있다.)
b. Fast Fourier Transform(FFT)
3번에서 노이즈캔슬링의 예시를 들었는데, 만약에 노이즈캔슬링이 느리다면 싱크가 안 맞는다던지, 오히려 외부의 잡음과 섞여서 잡음이 증폭이 되는 경우가 생길 수도 있을 것이다.
일단 적분하는 경우에는 당연히 시간이 많이 걸릴 것이고, DFT를 쓰면(직관적으로 그냥 계산하는 경우...), 이산적인 계산이니 적분보단 빠르게 계산을 하겠지만, 이를 좀 더 빠르게 계산하는 알고리즘들이 더 생겼는데, 이러한 알고리즘들을 Fast Fourier Transform이라고 한다.
--> 컴퓨터 계산에 최적화되기 위해 등장하였다고 볼 수도 있을 것이다!
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 14-2. 가끔씩 보이는 베타함수 (Beta Function) (0) | 2023.03.03 |
|---|---|
| (해석학) 14-1. 가끔씩 등장하는 감마함수 (Gamma Function) (0) | 2023.03.03 |
| (해석학) 13-2. 푸리에 급수가 그렇게 좋은가? (Convergence of Fourier Series) (0) | 2023.03.02 |
| (해석학) 13-1. 공대의 친구, 푸리에 급수(Meaning of Fourier Series) (0) | 2023.03.02 |
| (해석학) 12. 이만큼 배웠으니 급수가 다르게 보인다! (Analytic Function and Power Series) (0) | 2023.02.28 |



