이번 챕터에서는 공부하는 도중에 가끔씩 보이는 Gamma Function과 Beta Function에 대해서 알아본다....
먼저, Gamma Function의 경우, 대부분 Factorial(!)의 실수확장버전으로 알고 있을 것이다.
Gamma Function의 정의부터 알아보자!
(Gamma function)

우리가 앞에서 Improper Integral(해석학 8-5 참고)을 보았었는데, 이 정의를 이용해서 저 gamma function이 과연 수렴하는지 살펴보자.
(Convergence of Gamma Function)
비교판정법을 이용해서 Gamma Function이 수렴함을 보이면 된다!!!

t가 커질 때, 저 적분하는 함수가 1/t^2보다 작아지는 것을 이용하면 비교판정법을 이용해 수렴성을 판단할 수 있다!
(x는 그냥 주어진 값이고, exp(-t) 때문에 미친듯이 작아진다!)

이 경우에는,
t가 커지는 경우, 위와 마찬가지로 exp(-t) 때문에 똑같이 수렴성을 보이면 되고,
t가 0 근처에서 1/t... 형태라 문제가 되는데, 일단 exp(-t)가 1보다 항상 작고, (1/t)^(1-x)의 적분값이 항상 수렴한다는 것을 이용한다면(물론 x>0) 수렴성을 보일 수 있다! (여기선 s=1/t로 치환을 하였다!)
Gamma Function의 성질을 알아보자. -> Factorial의 확장보다 사실 더 중요한 성질을 가진다!
(Properties of Gamma Function)

여기서 Convex Function이라는 것이 나오게 되는데, (이미 대부분 알고 있겠지만) 정의는 다음과 같다.
(Convex Function)


어라라? 혹시 다음 정의를 생각하는가?

사실, 이 두 번 미분한 것을 이용한 정의는 정의라기보단 성질이다. -> 여기선, 일단 두 번 미분가능하다는 조건이 필요하다!
맨 처음의 정의에서 이 성질을 유도해보면...
(증명)
위의 Gamma Function의 성질을 증명하자!
(증명)
1. 부분적분을 이용하면 바로 나오는 사실이라 생략한다!
2.

인 것과, 1번 성질을 이용하면 바로 나오는 사실!
3.
우리가 증명할 건 다음과 같다!

이를 증명해보자! (해석학 8-5 참고!)
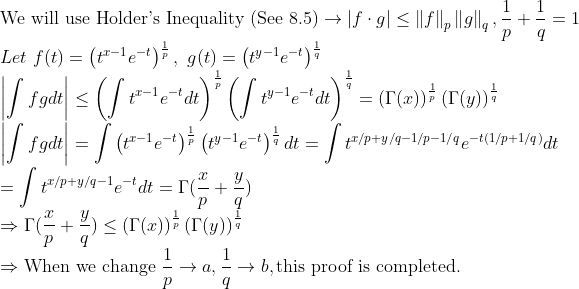
1번과 2번은 Factorial의 확장으로 볼 수 있고,
특히, 3번을 주목할 필요가 있는데, log 함수를 태우고도 Convex라는 것은, 이 Gamma Function의 증가율이 엄청나다는 것을 말해준다!! (심지어 Exponential 함수도 log를 태우면 선형인데....)
그런데, 여기서 주목해야 할건, 어떤 함수가 저 3가지 성질을 다 만족해버리면 (물론, 2번은 1번 만족하면 자동으로 만족) 그 함수는 무조건 Gamma 함수라는 것이다!!!
(Uniqueness Properties of Gamma Function)

(증명)
증명에서 헷갈리지 말아야 할건...??
1. 먼저, 우리가 Gamma 함수가 위의 3가지 성질을 보이는 것을 확인했다.
2. 여기선 저 3가지 성질을 만족하는 함수가 Unique(유일)하다는 것을 보일 것이다!
3. 그러니, 어떤 다른 f가 저 3가지 성질을 만족한다면, 그 함수는 무조건 Gamma 함수이다!
(0,1)에서 f가 유일하다는 것을 보이면, 주기성에 의해서(위의 1번성질) 양수 전체에서 유일할 것이다!
이 때, log f(x)가 Convex라는 것을 이용해서 증명하자!

여기서, Convex라는 성질을 이용하면, x가 커지면, 구간의 기울기의 값이 점점 커질테니(양수와 음수를 고려한다고 해도)
[n,n+1],[n+1,n+1+x],[n+1,n+2] -> 각각의 기울기를 비교한 것이 (*)이다!


위에서 비교판정법에 의해서 부등식 사이 값이 Uniform Convergence라는 것을 알 수 있다! (즉, x에 따라서 바뀌지 않는다!)
그러므로 phi(x)가 저 log의 lim 값임을 알 수 있고, "유일"하다!(phi(x) is unique!) -> 증명 완료!
또한, Uniform Convergence에 의해 그냥 우리가 log를 떼 줄 수 있으므로
Gamma Function의 값은 lim로 저렇게 써줄 수도 있다.(우리가 아는 적분 정의하고 다르다고 저게 Gamma Function이 아닌 게 아니다. -> 증명에서 헷갈리지 말아야 할건...??을 읽고 오자!)
여기까지 Gamma Function에 대해서 알아보았다.
알고 있던 것들도 있고, 모르던 것도 있을 수 있는데
1. log를 취해도 convex일 정도로 증가량이 크다는 것과,
2. 저 3가지 성질을 만족하는 함수는 Gamma Function 밖에 없다는 사실을 추가로 알아두면 좋다!
다음 시간엔 Beta Function에 관해서 알아보자!
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 15-1. 다변수벡터함수를 위한 선형대수1 (Linear Algebra for MIMO Function -> Linear Transformation) (0) | 2023.03.04 |
|---|---|
| (해석학) 14-2. 가끔씩 보이는 베타함수 (Beta Function) (0) | 2023.03.03 |
| (해석학) 13-3. 푸리에 급수의 응용 (Application of Fourier Series) (0) | 2023.03.03 |
| (해석학) 13-2. 푸리에 급수가 그렇게 좋은가? (Convergence of Fourier Series) (0) | 2023.03.02 |
| (해석학) 13-1. 공대의 친구, 푸리에 급수(Meaning of Fourier Series) (0) | 2023.03.02 |




