이번 챕터에서는 꽤나 어려웠던 이론 내용을 벗어나서 이론을 조금 응용한,
다변수함수에서 최댓값과 최솟값을 찾는 방법에 대해서 설명하고자 한다.
용어가 헷갈릴 수도 있어서 용어를 다시 정의해보자면
- 임계점(Critical Point) -> f'(x)=0이 되는 점
- 극값(Extreme value) -> 극댓값과 극솟값을 합쳐부르는 말
- 극댓값, 극솟값(Local extreme value) -> 국소적으로(Locally) 최대 / 최소 (자세한 정의는 아래 참고)
- 최댓값, 최솟값(Global maximum value) -> Domain의 모든 점에 대해(Globally) 최대/최소 (자세한 정의는 아래 참고)
(일변수함수의 최댓값과 최솟값)
고등학교 때, 미분가능한 일변수함수 y=f(x)의 최댓값과 최솟값을 어떻게 구하였는지 생각해보자.
1. 일단 미분해서 f'(x)=0인 x들을 찾는다. (임계점(critical point) 찾기)
2. 극점(x=p)에서
- f''(p)>0이면 아래로 볼록 -> 극솟값(극값)
- f''(p)<0이면 위로 볼록 -> 극댓값(극값)
- f''(p)=0이면 아무것도 아님(극값이 아님) (ex. y=x^3, x=0)
3. 극댓값 중 최대를 최댓값, 극솟값 중 최소를 최솟값으로 정하면 된다.
이러한 방식은 다변수함수로 와도 똑같다.
(다변수함수의 최댓값과 최솟값)
일단, 값을 비교하려면 output이 1차원이어야 할 것이다. 즉,

인 경우에만 가능하다.
먼저, 최대점/최소점의 정의는 다음과 같다.
(Global Maximum Point(최대점))

그리고, 이 점에서의 함숫값을 최댓값(Global maximum (value))이라고 한다.
여기서 최댓값과 최솟값의 존재여부는 일단 해석학 카테고리로 넘기기로 하자. (이미 아는대로, 닫힌구간에서 f가 연속이면 최댓값과 최솟값을 가진다.(최대/최소정리))
또한, 극대점과 극소점을 정의를 내려보자.
(Local Maximum Point(극대점))

즉, P가 극대점이라는 것은 P 주변(모든 방향)에서 f(P)가 가장 크다는 것을 이야기한다.
극댓값(Local Maximum (value))은 이 극대점에서의 함숫값을 의미한다.
극솟값도 이와 똑같은 방법으로 정의해주면 되고, 극값은 극댓값과 극솟값을 합쳐서 이야기한다.
즉, 정리하자면 우리가 아는 최댓값과 최솟값은 GLOBALLY MAX, MIN을 이야기하고, 극댓값과 극솟값은 LOCALLY MAX, MIN을 이야기한다.
일변수함수의 임계점은 f'(x)=0이 되는 point, 즉, 기울기가 0이 되는 지점으로 잡았는데, 다변수함수의 경우에는 기울기의 크기를 norm을 이용해서 정의하면 되겠다.
(Critical Point(임계점))
즉,
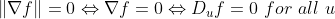
인 지점이 임계점이 된다.
그렇다면, 임계점과 극점은 같은걸까???
이미 일변수함수에서 보다시피 결론은 아니다. 그러나 일변수함수에서 우리는 이미 극점이 임계점임을 알고 있었다. 이를 다변수함수에서 증명해보자.
(Fermat's Theorem on Critical Point)
(Simply) 미분가능한 함수에서의 극점은 임계점이다. (역은 일반적으로 성립하지 않는다.)
(더 정확히는)
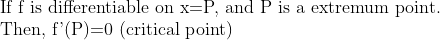
여기서의 요지는 P가 극점이므로, 극점의 정의에서 나온 Open set을 잡을 수 있다는 것이고, 이 것이 미분가능성과 합쳐저서 논리를 전개할 수 있다는 것이다.
(증명)
여기서는 극댓값인 경우만 증명한다. (극솟값일 때도 동일하게 증명가능)
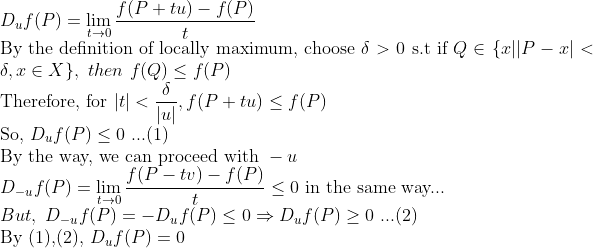
이 정리의 역은 우리가 일변수함수에서 보았듯이 (ex. y=x^3, x=0) 성립하지 않는다.
지금까지, 일변수함수에서 1번 과정을 다변수함수에서 증명해보았다.
이번에는 2번과정을 증명해보자.
위에서 극점과 임계점이 동일하지는 않기 때문에, 임계점에서 1.이를 거르는 과정이 일단 필요할 것이고, 2. 거른 것이 극대인지 극소인지 판단해야 할 것이다.
일변수함수에서는 이를 f''(x)를 통해서 알아보았다. -> 다변수함수에서는 이 것이 Hessian Matrix가 될 것이다.
그런데, 이 Hessian이 양수/음수 라는 것을 정의해야 하는데 어떻게 정의할까???
선형대수에 나오는 Positive/Negative Definite Matrix에 관한 내용이 필요하다...
다음에 나오는 설명은 선형대수에 관해서 아는 사람들은 보고, 잘 모른다 싶으면 아래에 나오는 정의만 보자...
(선형대수를 아는 경우)
Quadratic Form으로 설명할 수도 있고, 아니면 대각화(스펙트럼 정리)에 의해서도 설명할 수 있을 것 같은데, 여기서는 대각화를 이용한 설명을 하려고 한다. (결국엔 Positive Definite를 어떻게 정의하냐의 차이임)
Hessian Matrix를 H라고 하면 대각화(Diagonalization)를 통해서 주축(Principal axis)들을 찾아낼 수 있을 것이다.
그러면, 이 주축방향에 따른 lambda 값(eigenvalue)은 주축방향으로의 f''(x)라고 할 수있다.
그러므로 대각화를 했을 때의 lambda값들이
1. 모두 양수이면 아래로 볼록(극솟점) -> Positive Definite Matrix
2. 모두 음수이면 위로 볼록(극댓점) -> Negative Definite Matrix
3. 양수와 음수가 섞였으면 Saddle Point라고 한다.
이를 통해 아래의 2x2 행렬인 경우의 정의와 비교해보자.
만일, 대각화를 한다면,
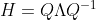
이 때, det H를 살펴보면 다음을 알 수 있다.
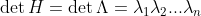
1. lambda가 모두 양수인 경우
det H>0, 또한,
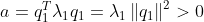
2. lambda가 모두 음수인 경우
det H>0 (2 by 2 행렬이므로), 또한,
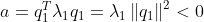
3. lambda가 양수 1개, 음수 1개인 경우
det H<0
(선형대수를 모르는 경우)
Hessian이 2x2 행렬인 경우에만 정의를 하자. (참고로 Hessian은 대칭행렬이다.)

1. a>0, det H>0이면 극소점
2. a<0, det H>0이면 극대점
3. det H<0이면 Saddle Point
여기서 Saddle Point라는 개념이 나오는데, 다음의 예를 하나 살펴보자.

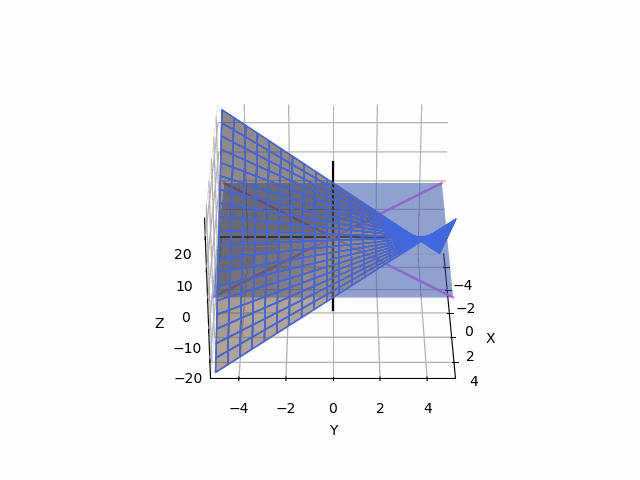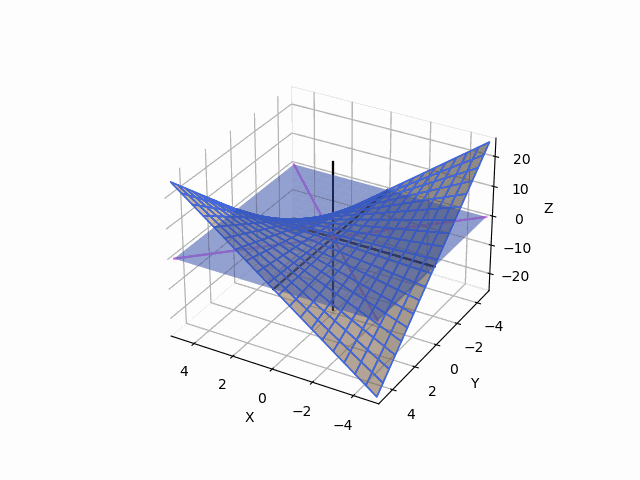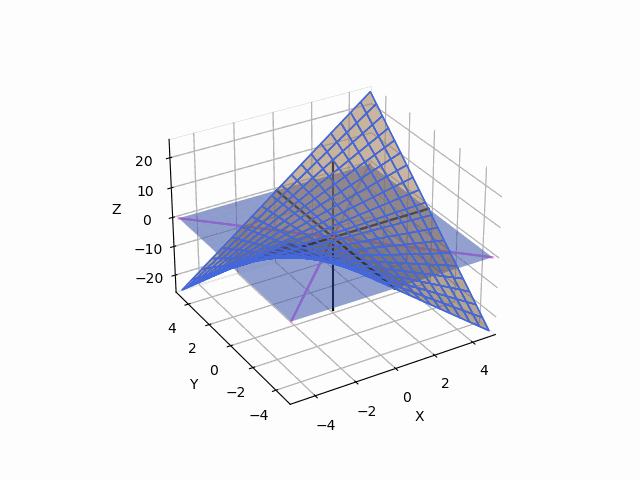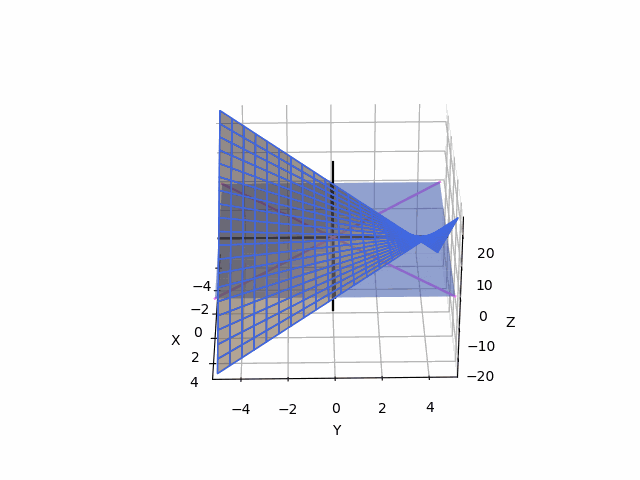
여기서, 그물로 된 그래프가 f의 그래프이고, 보라색 축이 y=x, y=-x (z=0)의 그래프이고, 검은색 축이 각 축이다.
1. y=x,z=0 방향으로는 극소점
2. y=-x, z=0 방향으로는 극대점
3. x축과 y축 방향으로는 사실 어떤 것도 아니다...
이렇게 방향에 따라서 극대로 보이기도 하고 극소로 보이기도 하는 점을 Saddle Point라고 한다.
(위의 선형대수 설명을 따르자면, 주축은 y=x, y=-x로 나오고, 각 lambda값이 y=x로는 >0, y=-x로는 <0이 나온다.)
그럼 위에 나온 내용들을 증명해보자.
(증명) (중요한 Quadratic Form에 대한 내용은 숨기지 않았다.)
n=2인 경우만 증명하지만, 선형대수 내용을 안다면, 이를 일반화시키는 것도 어렵지 않을 것이다. (그냥 Positive Definite 행렬 성질 써버리면 됨)

위에서는 Quadratic Form을 일종의 다변수함수처럼 생각할 수 있으므로 Q(x,y)에 대한 극솟점과 극댓점, saddle point를 정의에 의해서 구할 수 있었다.

여기서는 Quadratic Form을 이용해서, 일반적인 f(x,y)에 대해서 극솟점과 극댓점, saddle point를 구할 수 있었다.
자 지금까지 2번내용(f''를 통해 극대와 극소를 구별하기)을 하였고, 3번 내용(극댓값 중 가장 큰 것을 최댓값, 극솟값 중 가장 작은 것을 최솟값으로 잡자)의 경우에는 미분에 관한 내용이 아니라서 패스하도록 한다.
(사실, 극점의 집합은 countable이므로, 위의 내용이 성립할 수 있다.)
여기까지, 최댓값과 최솟값(극댓값, 극솟값)을 찾는 방법을 설명하였다.
사실, 증명이 많아서 그렇지 고등학교 때 배운 내용들을 그냥 다변수에 적용시킨 것밖에는 없다.
다음챕터부터는 미분에 관한 얘기가 아닌, 드디어 다변수함수의 적분에 관한 이야기를 다루겠다.



