(다변수함수의 고계미분)
다변수함수의 테일러정리를 위해 일변수함수의 테일러 정리를 생각해보자. 이를 보면, n번(nth-order) 미분한 함수가 필요한 것은 당연하다.
다변수함수의 이계 미분(Second-order)을 생각해보면, 일단, 도함수(전미분)가 행렬함수로 나타내어지니, 이를 다시 input으로 넣으면서 생각하기가 복잡해진다....
그러나 저번 챕터의 마지막 부분을 잘 생각해보면, 이 행렬함수를 풀어 써서 하나의 벡터로 볼 수 있기 때문에(물론, 3차원 텐서를 이용해서 논리를 전개할 수도 있겠지만) 이를 잘 이용하면, 이계 미분의 성분들은 다 구할 수 있다. 이 성분들을 잘 정리해서 이용하면, 마치 일변수함수 이계도함수처럼 사용할 수 있다. 그러나, 이런 방식(특히, output이 여러개(multiple dimension))인 경우에는 분야에 따라서 정의를 다르게 하는 경우도 많은 듯하다.... 또, 잘 안 쓰기도 하고...
사실, 테일러 정리를 사용하는 이유는 대부분 근사(approximation)인데, 대부분 선(line)이나 면(plane)에 대해서 주어진 1차원 함수 f(x)를 다항함수(Polynomial)꼴로 근사해서 사용하기 위함이라, output의 dimension은 1이 된다.
그래서 우리는 output의 dimension이 1인 경우, 즉,
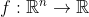
인 경우의 고계(High-Order) 미분만 생각해보려고 한다.
(다변수함수의 Second-Order Differentiation -> Hessian)
output의 dimension이 1인 경우의 전미분(Gradient)은 앞 챕터에서 본 바와 같이,
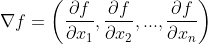
이 도함수의 미분은 앞 챕터의 내용을 이용하면,
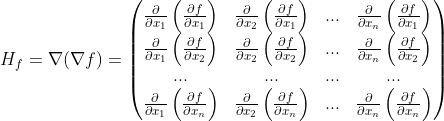
여기서 이계 미분 matrix H를 Hessian (Matrix)라고 한다.
또한, 각 성분은 다음과 같이 쓸 수 있다.
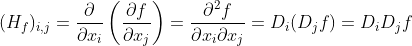
물론 이 표현을 확장하여 n계 미분도 표현할 수 있다.
여기서 중요한 성질 하나를 알고 넘어가자.
(Commutative Rule of Partial Derivatives)
편미분은 교환법칙이 성립한다.
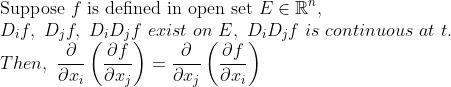
(증명)
편미분을 정의대로 펼쳐서 순서만 바꾸는 것으로 증명이 가능하다.
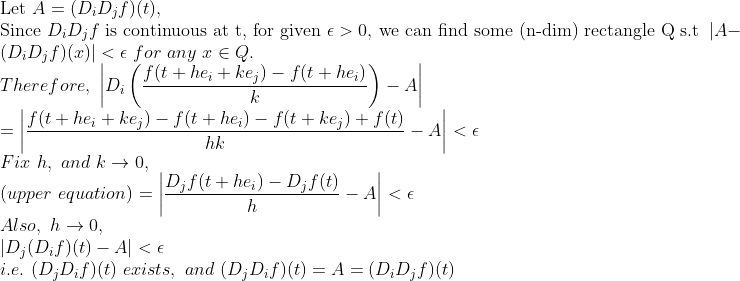
여기서 n-dim rectangle이 나오는데, 마치 다변수함수의 연속처럼 생각해서, n차원에서 i, j축만 delta radius를 가지고, 나머지 축은 그냥 마음대로 (즉, 3차원이면, 주어진 domain 내부에서 사각기둥처럼 주어질 것임) 주어진 도형으로 생각하면 된다.
(NOTE) Mean Value Theorem in Partial Derivative
위의 증명에서 순서바꿔서 편미분으로 바꾸는 과정을 일종의 Mean Value Theorem으로 생각할 수도 있다. 즉,
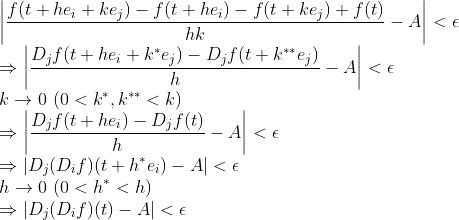
그러므로, 편미분은 교환법칙이 성립하고, Hessian은 Symmetric Matrix임을 알 수 있다.
자, 다음으로 고계(High-order)미분에 대해서 더 알아보자.
일변수함수일 때, 테일러 정리를 살펴보면,
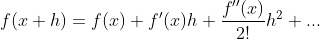
여기서 다변수함수로 확장하면, x,h가 벡터로 변환이 되는것이고, 미분(기울기)은 h의 방향미분으로 확장이 된다.
그러면, 여기서 우리가 필요한 미분은 h 방향미분을 n번한 것이 필요하다.
즉,
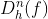
가 필요하다.
이미,
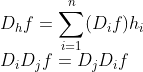
를 알고 있으므로,
(High-order Directional Derivative)
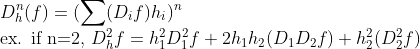
이런 식으로 표현할 수 있다.
다음에는 이를 이용한 다변수함수의 테일러 정리에 대해서 알아보자.



