일변수함수의 테일러 정리는 다음과 같았다.
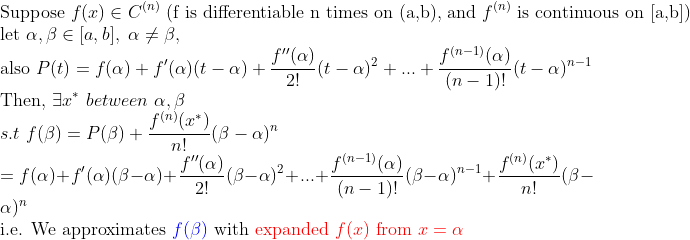
이번에도 이와 같은 방식으로 테일러 정리를 유도해보자.
(Taylor theorem in Multivariate Function)

(증명)
사실,

로 놓으면, g는 일변수함수이므로, t=0에 대해서 테일러 정리를 쓰면 바로 증명이 가능하다.
(Note)

또한, k차 테일러 전개에서의 오차는 일변수함수와 동일한 방식으로
(Error of k-th-order Taylor Expansion)

더 나아가, k-norm을 다음과 같이 정의하는데,

이를 위의 Error 식과 종합해보면

지금까지는 테일러 정리에 관한 내용이고, 여기서 몇가지 더 테일러 전개(Taylor Expansion)의 성질을 알아보도록 하자.
여기선 편의상 일변수함수에 대해서 생각해보자.

1. 테일러 전개는 유일하다. (Uniqueness)
(증명)
테일러 정리에 의해서 다음과 같은 식이 성립한다.

만일, 다른 k차 다항함수 P(x)도 이를 만족한다고 하자.(그러면 테일러 정리에 의해 P(x)도 또 다른 테일러 전개이다.) 즉,

그럼, 두 식을 빼면, at most 최고차항이 k차항이므로,

그러므로, 테일러 전개는 각 k에 대해서 유일하다.
또한,
2. k차 테일러 전개가 k차 다항함수 꼴로 나타낸 가장 최적의 근사
임을 알 수 있다.
그 이유는, k차 테일러 전개를 한다면, k차 다항함수로 표현이 될텐데, 다항함수를 가지고는 더 오차를 줄일 방법이 없다.
(테일러 정리에 의해서 x, x^2, ..., x^k항을 아무리 더하고 빼보았자 오차에는 아무런 영향을 줄 수 없다.)
즉, k차 테일러 전개에서 더 오차를 줄이기 위해서는 x^(k+1)항이 필요하다.
그러나 이는 더이상 k차 테일러 전개가 아니다. 그러므로 위의 성질을 알 수 있다.
사실, 실용적으로는 1차 근사식과 2차 근사식 정도나 쓰고, 그 이상의 근사식은 사실상 쓰기 어렵다.(3차 이상의 도함수를 구하기 위해선 연산이 너무 많아짐, 그래서 2차 근사식도 잘 안씀...)
이론적으로 더 알아보고 싶다면, 추가적으로 선형대수나 해석학을 참고하기 바란다.
다음챕터에서는 gradient와 hessian을 배웠기 때문에, 미분의 활용, 즉, 최대/최솟값을 구하는 문제를 설명하도록 하겠다.



