지난 챕터에서는 2차원 평면에서 극좌표계를 다뤄보았는데 이번시간에는 3차원 공간의 실린더 좌표계와 구면 좌표계를 소개한다.
(Cylindrical Coordinate System(실린더 좌표계))
3차원 공간의 좌표(x,y,z)를
1. 주어진 좌표와 z축과의 거리(r)
2. 주어진 (x,y)와 x축과의 각도(theta)
(1,2는 주어진 z의 z평면에서 극좌표계로 변환하는 것과 동일)
3. 나머지 (z)
로 표현한 좌표계로 이를 표현하는 변환(Transformation)은 다음과 같다.

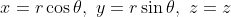
단지, z좌표만 제외하고 극좌표계로 바꾸는 것과 동일하다.


(Spherical Coordinate System(구면 좌표계))
3차원 공간의 좌표(x,y,z)를
1. 원점으로부터의 거리(r)
2. (x,y,z)과 z축과의 각도(phi)
3. (x,y,0)과 x축사이의 각도(theta)
로 표현한 좌표계로 이를 표현하는 변환(Transformation)은 다음과 같다.


잘 이해가 안 간다면 아래에 있는 그림을 보면 r,phi,theta가 무엇을 뜻하는지 바로 알 것이다.

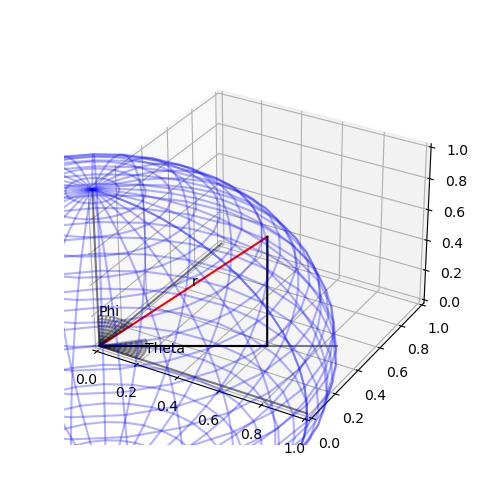
2차원 좌표계에 대한 것은 복소수에서 조금 써먹었는데, 3차원 좌표계에 대한 것은 아직 잘 와닿지 않을 수 있다.
그러나, 나중에 선적분, 면적분 등을 배울 때 이러한 좌표변환을 이용하면 식을 깔끔하게 만들 수 있고, 쉽게 적분할 수 있어서 좌표계에 관한 내용은 필수이므로 꼭 기억하자.
다음 챕터에서는 다변수함수의 연속이나 미분에 관해서 살펴보도록 한다.



