미적분학 초반 챕터에서는 수열과 일변수함수의 극한(수렴)을 다뤘었다.
여기서는 다변수함수의 연속과 미분에 대해서 설명한다.
사실 초반 챕터(일변수함수)와 크게 다를 건 없으니 초반에 이해를 잘 했다면 문제 없이 넘어가니 걱정말자.
먼저 수열의 극한에 대해서 다시 한번 보자.

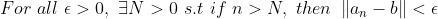
사실 앞에서 이걸 설명할 때, 수열{a_n}이 정의된 곳과 b를 그냥 실수(real number)인 것처럼 대충 넘어갔지만, 굳이 {a_n}과 b가 실수일 필요는 없다. 그냥 저 Metric(거리)만 잘 정의되면, 그 metric space 안에 {a_n}과 b가 있으면 되는 것이다. (해석학 참고)
예를 들어서, b가 2차원 벡터(0,1)여도 상관이 없고, 3차원 벡터(1,3,2)여도 상관 없다. 그냥 한 점(point)이면 된다. 1번 챕터에서 본 gif를 생각하면 된다.(2차원)
그렇다면 이를 이용해 다변수함수의 극한을 생각해보자.
(다변수함수의 극한)

이 경우에도 일변수함수의 극한과 같은 방법으로 정의할 수 있다.

단지 전에 보았던 x,a(p),b가 그냥 m, n차원으로 바뀌었을 뿐이다...
(다변수함수의 연속)
이 경우에도 일변수함수의 연속과 같은 방법으로 정의할 수 있다.
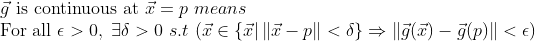
일변수함수에서의 연속함수의 성질들도 그대로 유지한다. (딱히 바뀐게 없으므로....)
그러나 다변수함수로 오면서 이 성질은 추가된다.
(다변수함수의 연속과 성분함수의 연속 관계)
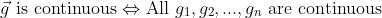
(증명)
1.
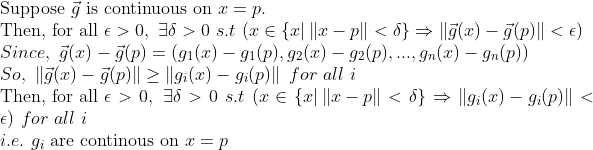
2.

이 때, metric(norm)의 성질을 이용해서 증명하였다.
여기까지 다변수함수의 극한과 연속을 보았다. 수열의 극한을 그냥 차원만 올려서 보는 것만으로도 다변수함수의 극한과 연속을 쉽게 다룰 수 있었다. 다변수함수의 미분은 똑같을까? 다음 챕터에서 확인하자.



