(NOTE)
본 내용은 수학적인 내용보다는 공학적인 내용에 조금 더 초점을 맞추고 있습니다. 그리고 추상대수학의 "군(Group)"에 대한 내용이 나오는데 이는 추후에 추상대수학 카테고리에서 자세히 다룰 예정이고, 여기서는 다루지 않을 예정입니다. 최대한 빠르게 추상대수학 카테고리 내용을 업로드하도록 하겠습니다!
우리는 앞에서 Orthogonal Matrix(복소수에서는 Unitary Matrix)를 보았다.
물론 Spectral Theorem을 사용하기 위해서라도, Orthogonality가 아주 중요한 개념이 되기는 하지만, 이를 다른 방면으로 응용할 수도 있다.
먼저, Orthogonal Matrix(혹은, Unitary Matrix)를 선형변환(Linear Transformation)으로 보았을 때, 우리는 다음 성질을 보았었다.
1. Orthogonal(Unitary) Matrix로 인한 변환 전후의 Norm은 동일하다. 즉,

2. Orthogonal(Unitary) Matrix로 인한 변환 전후의 내적은 동일하다. 즉,

일단, "실수" 행렬 -> Orthogonal Matrix로 한정해서
Orthogonal Matrix의 행렬식을 구해보자.
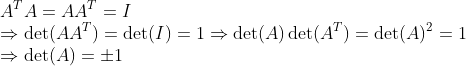
즉, 행렬식=1 or -1이 된다.
그런데, "좌표계 변환"의 관점에서 행렬식의 절댓값(즉, Jacobian!)의 의미는 => "미소부피의 변화"이다. (미적분학 16-3 참고!)
행렬식이 1이라는 것은 "부피 보존"을 의미하고, 위의 "NORM 보존, 각도 보존"의 의미 또한 생각한다면,
=> 회전 변환을 말한다!!
ex)

행렬식이 -1이라는 것은 한 면을 기준으로 거울에 비치는 것처럼 뒤집히는 것, 즉 반사(Reflection)를 말한다.
ex)

그렇다면, 만약에 원점에 고정되어있고, 어디로든 회전가능한 길이가 고정된 로봇팔 끝 부분의 위치를 표현하려면, 어떤 회전변환이 필요할까...?
1. 로봇팔 길이가 고정 => Norm이 보존되어야 한다.
2. 로봇팔 회전 => 각도가 보존되어야 한다.
3. 그러나, 로봇팔의 움직임에 "반사"는 없어야 한다! => 행렬식이 1이어야 한다.
4. 또한, 위치는 항상 실수 => 실수행렬!

=> 결론을 내리자면
행렬식이 1인 3차원 실수 Orthogonal Matrix가 로봇팔 끝 부분의 위치를 표현한다. 이러한 변환의 모음을 SO(3)이라고 한다.
조금 더 일반적으로 정의해보자.
(Special Orthogonal Group) => SO(n)
행렬식이 1인 n차원 실수 Orthogonal Matrix의 모음을 SO(n)이라고 한다.
더 정확히 말하자면 다음 군이 SO(n)이라는 말은

여기서 G는 집합(결국 n by n orthogonal matrix, determinant=1인 행렬들의 모음이라고 생각하면 된다.)
그리고, 점(.)은 행렬곱을 뜻하는 연산이라고 생각하면 된다.
또한, 리 군(Lie Group)에 대한 내용이 나오는데, 간단하게 저 집합(공간) G에 대해서 "무한번 미분"이 잘 정의되어 있다(매끄러운 다양체; Smooth Manifold)고만 생각하자.
복잡하다면 그냥 행렬식이 1인 n차원 실수 Orthogonal Matrix가 SO(n)이라고 생각하자!
여기에 더해서, SO(n)은 n차원 "회전변환"의 모음이라고 생각할 수 있다.
그러면, 복소수행렬(즉, Unitary Matrix)으로 위의 내용을 대체할 수는 없을까?
이번에도 Unitary Matrix의 Determinant를 구해보자. 그러나, "복소수" 행렬이기 때문에, Determinant가 "복소수"가 튀어나올 수 있다는 점에 유의하자!
Determinant = (Eigenvalues의 곱)(11-1 참고), Unitary Matrix는 Normal Matrix이므로 Diagonalization이 가능(13-2 참고)
이를 이용하면,

위의 실수 행렬보다 더 "넓은 의미"가 된다. 왜냐하면 determinant의 "크기"가 1이면 되기 때문이다.
그러나, 이를 다시 "회전변환"의 의미로만 좁힌다면, 위처럼 determinant=1로 한정시키면 된다. 이러한 Unitary Matrix Group을 SU(n)이라고 한다.
(Special Unitary Group) => SU(n)
행렬식이 1인 n by n 복소수 Unitary Matrix의 모음을 SU(n)이라고 한다.
(Property)
SU(2)에 있는 행렬들은 다음과 같이 표현된다.

(증명)


이를 다시 정리하면 결국 A는 다음 꼴로 표현된다는 것을 알 수 있다!!!

그런데, 한번 잘 생각해보자.
1. SU(2)의 원소 하나를 결정하기 위해서는 두 개의 복소수가 필요하다. => 4개의 Independent Variable(각 복소수마다 실수, 허수파트)
2. 그런데, Norm 조건 1개를 만족해야 한다.
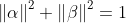
=> 그러므로, 1개의 Independent Variable은 Dependent로 변화한다.
=> SU(2)의 경우 "3개의 자유도"를 가지고 있다.
=> 즉, SO(3)과 SU(2)는 표현방식만 다르고, 회전변환을 나타내는 행렬이다!!
*(더 자세한 내용은 추상대수학의 동형사상(Isomorphism) 참고!)
게다가, 잘 생각해보면 쿼터니안(Quarternion)과 관계가 있다는 것을 알 수 있다.
=> Unit Quarternion(즉, 길이가 1인 쿼터니안) => 3차원 자세 표현할 때 사용한다!!!

(NOTE)
SU(n)에서 n은 결국에는 로봇팔이 존재하는 공간의 차원과는 무관해도 된다!!! => 오히려 모션의 자유도에 의해서 결정!
(물론, SO(n)도 로봇팔이 존재하는 공간의 차원과는 무관하게 생각할 수도 있다. 그러나 SO(3)의 경우에는 너무 직관적...)
추가로, 아래 그림과 같은 상황을 생각해보자. 즉, 로봇팔 하나(빨간색)의 끝에 또 로봇팔(파란색)이 달려있는 상황이다.

그러면, 이 상황에서 자유도(DOF; Degree of Freedom)는 어떻게 될까??
일단, 원점에 고정된 빨간색 로봇팔의 자유도는 각 축의 회전으로 3
그리고, 파란색 로봇팔의 자유도는 "빨간색 로봇팔이 고정되어 있다면" 당연히 3이다.
그러므로, 3+3=6 DOF를 가진다!
(NOTE)
3x3=9 DOF가 아니다!
왜냐하면, (빨간색 x축방향 돌린 후, 파란색 x,y,z축으로 따로 돌려버리고), (빨간색 y축 -> 파란색 x,y,z축 돌리는),..... 모션이 아니라
빨간색 위치가 정해지면(즉, x,y,z축으로 다 돌려버린 이후), 그 이후에 파란색을 돌려버리는(x,y,z축으로 돌리기) 모션이기 때문!
그러면 이때의 로봇팔의 자세는 어떻게 표현가능할까??? 아래의 예시를 보면서 생각하자.
ex) 빨간색 로봇팔의 길이=1, 파란색 로봇팔의 길이=0.5
빨간색 로봇팔 끝 위치 x, 파란색 로봇팔 끝 위치를 y라고 하자. 그리고 초기 위치를 다음과 같이 잡자.

z축방향으로 빨간색 로봇팔을 45도 돌렸다고 하자. => 빨간색 로봇팔 끝 위치를 x_1이라고 하자. 또한, 파란색 로봇팔 끝 위치를 y_1이라고 하자.

그리고 이번에는 빨간색 로봇팔에 붙어있는 좌표계를 기준으로 파란색 로봇팔을 y축 방향으로 45도 또 돌렸다고 하자. => 파란색 로봇팔 끝 위치를 x_2이라고 하자. 또한, 빨간색 로봇팔 끝 위치를 y_2이라고 하자.

그러면, 저 y_2를 만드는데, 빨간색 z축으로 45도, 파란색 y축으로 45도 => 이 한 가지 경우 밖에 없을까????
당연히, 그렇지 않다!!! 다음 그림을 보자!

즉, 로봇팔의 자세는 다르지만, 끝 점은 동일할 수도 있다.
=> 만일, 로봇이 움직이는 범위가 한정이 되어있다고 할지라도, Joint가 늘어나면, 어떤 목표지점을 향하는 것의 가능성이 증가!!
(NOTE)
로봇팔을 "최적의 경로"로 움직이는 것도, 위의 이유때문에 여러 가지 방법이 있을 수 있다. 다만, "최적"이라는 표현을 수학적으로 표현하기 위해서, 어떤 성능 값을 Heuristic(즉, 사용하는 사람의 편의에 따라서)하게 잡아서 그것을 최대화, 혹은 최소화시키는 방법으로 로봇팔의 자세 경로(trajectory)를 결정한다.
다시 문제로 돌아온다면...
=> SU(2)가 로봇팔 1개의 자세를 표현하므로, 저렇게 Joint가 존재하는 경우에는
=> SU(2) x SU(2)와 같은 식으로 위 경우의 자세를 표현하면 될 것이다!!!
이외에도, SO(n)과 SU(n)은 전자의 스핀이나, 양자색역학에도 쓰인다고 한다....
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 부록 2-1. Beginning of Optimization Problem (1) | 2023.11.05 |
|---|---|
| (선형대수학) 16. Matrix Norm(행렬 Norm) (1) | 2023.10.29 |
| (선형대수학) 15-2. Singular Value Decomposition을 이용해보자! (1) | 2023.08.31 |
| (선형대수학) 15-1. Intro. of Singular Value Decomposition (0) | 2023.08.30 |
| (선형대수학) 14-3. Principal Axis Theorem, Sylvester's Law of Inertia (1) | 2023.08.29 |



