이번에는 Quadratic Form과 Positive Definite Matrix을 이용한 성질을 조금 더 알아보도록 하자.
1. Principal Axis Theorem(주축 정리)
이 정리는 Quadratic Form의 항들이 적절한 변환을 통하면 xy등의 거치적거리는 항들이 모두 x^2, y^2과 같은 2차항으로 표현된다는 것을 말해준다. (Positive Definite Matrix는 필요 없음!)
즉, 복잡하게 주어진 2차곡선에 대해서 변환만 잘해버리면 심플하게 주축이 x축, y축을 가지도록 변환할 수 있다!!!

먼저, 증명을 해보고 예시를 들어본다!
(증명)
주어진 Quadratic Form에 대해서 A를 Symmetric 하게 잡을 수 있으므로 Diagonalization을 하면 다음과 같다.
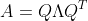
그러므로,

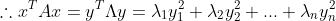
결국 이 증명과정에서 알 수 있는 것은...
1. y가 Principal Axis(주축)이 되어버린다! 그리고 축의 각도를 항상 유지한다! (Q는 Orthogonal => 내적 보존! => 각도 유지)
2. 이 때, 각각의 Eigenvalue의 값에 의해서 각 축의 길이가 변화한다!
ex)
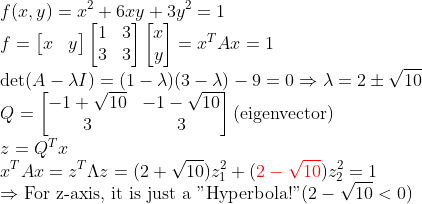
주어진 이차곡선이 마치 "타원"처럼 보일수도 있지만, 실제로 계산해보면, 쌍곡선이 나온다는 사실을 알 수 있다!!
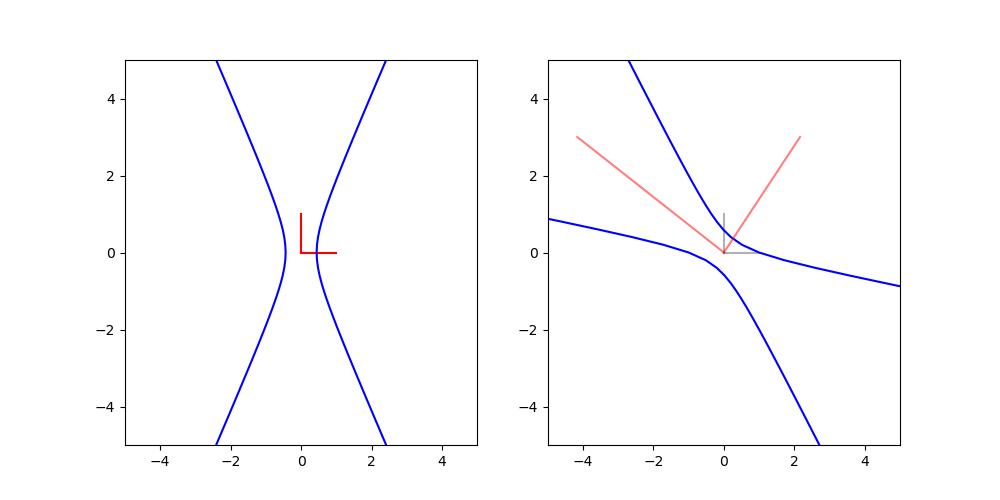
(여기서 오른쪽 곡선이 f에 해당하는 곡선이고, 왼쪽은 z축 관점에서 본 곡선이다.)
그렇다면, 여기서 더 나아가서 A가 Positive Definite Matrix라면..??
1. Eigenvalue가 모두 양수 -> 축을 변환할 때, 축의 방향이 바뀌지 않는다!
2. 저 Quadratic Form이 양수가 나온다! -> 이차곡선을 해석할 때, 계수의 부호가 바뀌지 않아도 된다!
=> Ellipsoid(타원)을 말한다!
그러므로, Positive Definite Matrix에 해당하는 Quadratic Form은 항상 Ellipsoid를 만족한다!
2. Sylvester's Law of Inertia
실제로 관성의 법칙을 뜻하는 것은 아니고, 위처럼 Symmetric Matrix에 대해서 Diagonalization이 가능할 때, 마치 Similarity Transformation처럼 다음 변환을 생각해보자. (A가 Invertible이라는 가정을 하자.)

(이 때 S는 eigenvector일 필요는 없다. 즉, D가 Eigenvalue 행렬일 필요도 없다.)
이러한 변환을 Congruent Transformation이라고 한다.
이 경우 D와 A의 eigenvalue를 비교해보면
1. 양수인 eigenvalue의 개수가 동일
2. 음수인 eigenvalue의 개수도 동일
3. 0인 eigenvalue의 개수도 동일하다.
이를 Sylvester's law of Intertia라고 한다.
이를 증명해보자!
(증명)
A가 Symmetric이면, Eigenvalue가 항상 실수로 나오므로, Diagonalization을 했을 때, eigenvector의 크기만 잘 맞추어준다면, Eigenvalue 행렬의 성분들을 모두 1, 0, -1로 만들어줄 수 있을 것이다.
이렇게 나온 Eigenvector 행렬을 Q라고 하자. 그러면
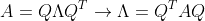
자 그러면 우리가 임의의 S와 주어진 Q에 대해서 S를 Q로 서서히 만들어주는 한 연속함수를 생각해보자. 즉,

이 때, 이러한 연속함수를 항상 만들 수 있는지 잠깐만 생각해보자.
=> Gram-Schmidtz를 이용해보자! (A가 Invertible하므로...)
S가 주어졌을 때, Gram-Schmidtz를 이용해서 QR-Decomposition을 해보자.

즉, 항상 invertible한 연속함수를 잡아낼 수 있다!
그렇다면, 어쨌든 저런 연속함수를 잡아낼 수 있으므로, t=0 -> 1로 변화되는 동안에는
1. 항상 S(t)가 Invertible하고 (즉, eigenvalue가 0이 되지 않는다.)
2. 연속이기 때문에, eigenvalue도 당연히 연속적으로 움직인다.
=> 그러므로 S(t)가 t가 움직이는 동안 0인 Eigenvalue를 건드리지 않으므로, Q(Eigenvector 행렬)의 양수/음수/0 인 eigenvalue의 개수도 그대로 동일하다!
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 15-2. Singular Value Decomposition을 이용해보자! (1) | 2023.08.31 |
|---|---|
| (선형대수학) 15-1. Intro. of Singular Value Decomposition (0) | 2023.08.30 |
| (선형대수학) 14-2. Quadratic Form과 극값 판별 (0) | 2023.08.28 |
| (선형대수학) 14-1. Definition of Positive Definite Matrix (0) | 2023.08.17 |
| (선형대수학) 13-2. Spectral Theorem (0) | 2023.08.03 |



