지난번에
Positive Definite Matrix에서

인 것을 생각해보면,
Positive Definite Matrix는 마치 "2차식(더 정확히는 Quadratic Form)"처럼 생각할 수 있다는 것을 느낄 것이다.
라는 내용을 보았다.
먼저 위에서 나온 Quadratic Form에 대해서 정의하자.
(Quadratic Form)

그냥 모든 항의 차수가 2인 Polynomial을 Quadratic Form이라고 말한다. (그러나, 항의 차수가 1인 것이 있으면 안된다!!!)
그런데, 이 Quadratic Form을 Matrix를 이용해서 표현할 수 있다.
(Matrix Expression of Quadratic Form)

즉, Positive Definite Matrix에서 보았던 바로 그 꼴로 나타내어진다는 것을 확인할 수 있다!!
또한, 여기서 당연하게 저 A에 의해서 Quadratic Form이 정해진다는 것을 알 수 있다. -> A가 Quadratic Form의 성질을 결정한다!
예를 들어, A가 Positive Definite Matrix이면, 당연히 Quadratic Form으로 나타내어진 식도 0보다 큰 것을 알 수 있다.
그런데, Quadratic Form에서 저 A는 항상 Symmetric으로 잡아버릴 수 있다!! (A는 실수행렬이라고 가정하자)
(증명)
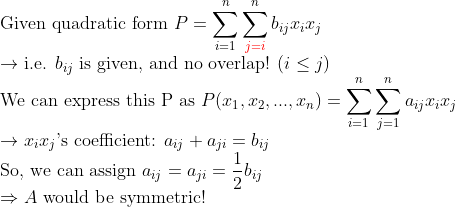
그러므로, 이제부터 Quadratic Form이라고 했을 때, A는 항상 Symmetric으로 생각한다!
우리가 이제부터 중점적으로 볼 것은 Quadratic Form의 최대/최소 문제이다.
먼저, Quadratic Form의 최댓값과 최솟값이 어느 point에 있는지 알아내기 위해서 미분을 해보자!

그러므로 적어도 x=0가 극점이 된다!
그러면, 이 x=0에서 f가 최댓값 / 최솟값 / 혹은 아무것도 아닌지(Saddle Point) 확인해보자.

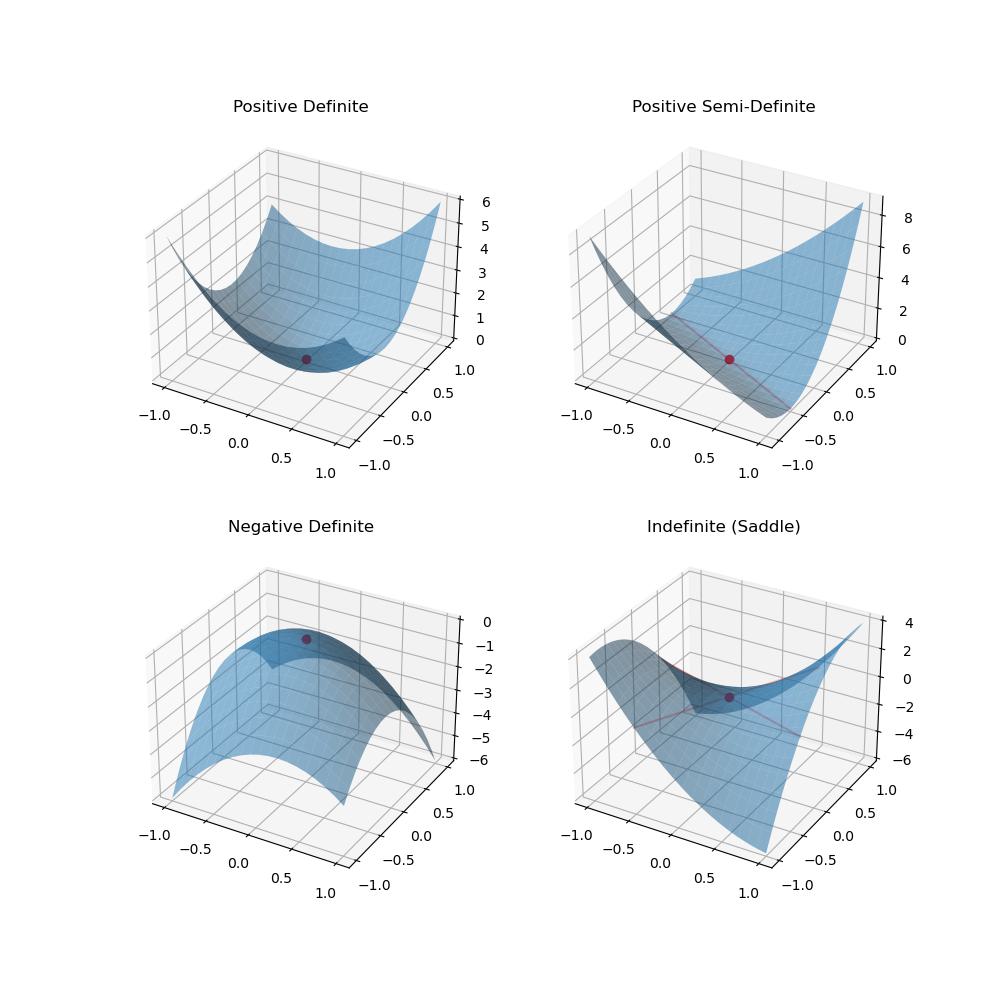

(위에서 빨간 선은 극점이 되는 Ax=0인 Point)
Indefinite Matrix라는 것은 Positive Definite도 아니고, Negative Definite도 아닌 경우를 말한다. (단, 여기서 Symmetric 조건은 유지)
1,3은 너무 당연한 이야기이고, 4번(Indefinite Matrix)을 통해서 조금 더 자세히 설명해보자.
Symmetric이므로 12-2에서 본 내용대로 eigenvalue가

Indefinite Matrix는 양수, 음수 Eigenvalue를 동시에 가지고 있으므로,
위의 값은 어떤 eigenvector x에 대해서는 양수값, 또 다른 eigenvector에 대해서는 음수값을 가져야 한다.
그런데, 위의 식을 보면 알겠지만, eigenvector의 크기는 eigenvalue값에 영향을 주지 않는다.

즉, 중요한 건 eigenvector의 방향이다.
그러므로, 원점 주위에서 "방향"에 따라서 eigenvalue, 즉 x^HAx의 값이 양수가 되거나 음수가 된다.
즉, 방향에 따라 Maximum Point가 되기도 하고, Minimum Point가 되기도 하는 Saddle Point가 된다!
2번(Semi-Definite)의 경우에는, eigenvalue에 0을 가지고 있다는 말인데, 이 경우에는 A가 Full-rank가 될 수 없다! (즉, 역행렬이 존재할 수 없다!)
그러므로 위에서 Ax=0의 해가 x=0 하나만 나오지 않고 원점을 포함한 직선이나 평면 등.... 이 나오게 된다.
=> 이 라인이나 평면을 기준으로 일종의 극"선"이 되거나 극"면"이 된다!
더 나아가서, 이를 다변수함수의 미적분에서 생각해보자...
(만일, Gradient, Hessian에 대해서 모른다면 -> 미적분학을 보고 오자! => 일단은 Positive Definite가 아래처럼 쓰인다는 정도만 알면 된다!)
어떤 다변수함수 F가 있다고 생각해보자.

그러면, 이 F를 "한 번" 미분하면 => 벡터(Gradient), "두 번" 미분하면 => 행렬(Hessian)이 튀어나올 것이다.
그런데, 이 미분을 이용하는 가장 대표적인 정리가 바로 테일러 정리일 것이다.
(테일러 정리 -> 원래함수 F를 "어떤 점"에서 Polynomial 형식으로 근사!)
그러면, 이 F에 대해서 테일러 정리(원점 기준)를 사용해보자!
(F 값이 실수로 나온다는 것에 유의하면서 차원을 맞추어가면서 전개하자!)

테일러 정리를 통해서 구한 "2차항"이 Quadratic Form으로 나오는 것을 확인할 수 있다!!!
이 내용을 어떻게 응용할까???
1. 만약에 우리가 F(x)를 그냥 2차항까지로 근사시킨다면

2. 그런데, 우연히도 앞의 상수항과 1차항이 모두 0이 되어버린다고 생각해보자!


그러면 A에 따라서 F의 최댓값이나 최솟값을 파악할 수 있다!!
물론 이 가정이 되게 빡빡하게 느껴질 수 있다! 하지만, 국지적으로(Locally) 저렇게 2차항으로 잡아도 오차가 크게 나지 않는 영역(오차가 선형)을 어떻게든 잡아버릴 수 있기 때문에 (해석학 내용 참고) 비선형 F의 증가/감소 성질을 hessian을 통해서 국지적으로(Locally) 알아버릴 수 있다!!
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 15-1. Intro. of Singular Value Decomposition (0) | 2023.08.30 |
|---|---|
| (선형대수학) 14-3. Principal Axis Theorem, Sylvester's Law of Inertia (1) | 2023.08.29 |
| (선형대수학) 14-1. Definition of Positive Definite Matrix (0) | 2023.08.17 |
| (선형대수학) 13-2. Spectral Theorem (0) | 2023.08.03 |
| (선형대수학) 13-1. Similarity Transformation, Change of Basis (0) | 2023.08.03 |



