이번 챕터에선, Spectral Theorem을 살펴본다.
이 Spectral Theorem은 Hermitian(실수에서는 Symmetric) Matrix의 Diagonalization을 보장한다.
(NOTE)
항상 정사각행렬이 Diagonalization이 되는 것은 아니었다.... => 그럴 때는, Jordan Form!
(Spectral Theorem)
1. 실수 행렬인 경우
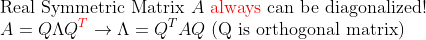
2. 복소수 행렬인 경우

그리고, 이렇게 Diagonalization이 되는 것을 Spectral Decomposition이라고 한다.
우리가 증명할 내용은 저 A가 항상 Diagonalized 되는지만 보면 된다! (나머지는 Hermitian의 성질에서 다 본 내용들)
이를 위해서 증명할 내용이 바로 Schur's Lemma이다.
(Schur's Lemma)
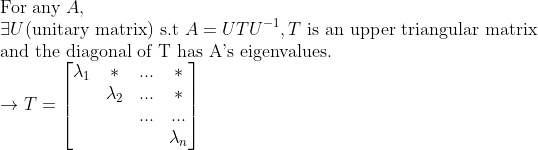
즉, 어떤 A이던지 위의 성질을 만족하는 unitary matrix U를 잡을 수 있다는 내용이다.
(증명)
먼저 A의 Eigenvalue Problem을 생각해보자...
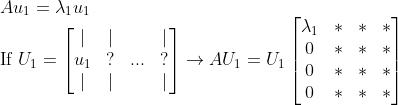
이 때, U_1에 들어갈 나머지 column들은 Gram-Schmidt 과정을 통해서 u_1과 서로 Orthogonal하게 나온 Basis들로 채우면 된다. 그러므로 U_1을 Unitary Matrix라고 할 수 있을 것이다....
그럼, 다음 스텝으로 넘어가보면
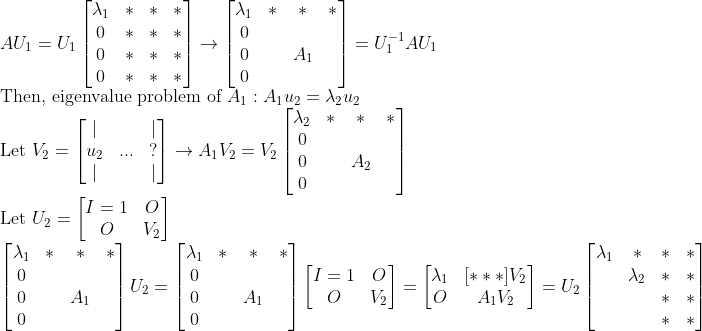
위에서 V_2 또한 Unitary Matrix로 잡을 수 있고, 저렇게 U_2를 구하면, U_2는 새로운 차원에 1이 채워지는 꼴이므로 Orthogonal Matrix(Unitary)를 만족한다.
즉, 행과 열을 하나씩 줄여나가면서 Eigenvalue를 구해보면, 계속 Lower 줄을 하나씩 0으로 바꿔나갈 수 있으므로, 이를 반복하면 결국에는 Upper Triangular Matrix T가 나올 것이다.
Schur's Lemma를 만족하는 것(언제나 Triangular Matrix로 바꿔주는 Unitary Matrix가 존재)과
Hermitian의 성질(항상 Diagonalization을 하면, Eigenvector Matrix가 Unitary)을 생각해보면, Eigenvalue Matrix는 항상 Triangular이므로
=> Hermitian은 항상 Diagonalization을 보장한다! (with Unitary Eigenvector Matrix)
(NOTE)
1. Jordan Form 증명에서는 Unitary 조건이 없다!! => 서로 다른 문제임
2. Schur's Lemma는 중복되는 Eigenvalue에도 그대로 사용이 가능하다! => Jordan Form하고는 다르다!!
그런데, 앞 챕터에서 보았듯이, 이는 Hermitian(Symmetric)에만 국한되는 내용은 아니다.
왜냐하면, Skew-Symmetric, Orthogonal matrix에서도 Eigenvector Matrix가 Unitary로 나오는 것을 보았었기 때문이다.
그러면, 이 세가지 유형(Hermitian, Skew-hermitian, Unitary)에서만 이 내용이 적용이 가능한가??
=> 아니다!
조금 더 확장해서 Normal Matrix면 가능하다!
=> 즉, Normal Matrix는 항상 Diagonalization이 가능하다!
(Normal Matrix)
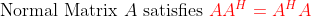
위의 세가지 유형을 대입해보면 알겠지만, Symmetric, Skew-Symmetric, Orthogonal 모두 Normal Matrix의 일종이다.
그러면, Normal Matrix가 항상 Diagonalization이 가능하다는 것을 증명해보자.
(증명)
먼저, Schur's lemma에 의해서
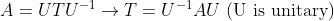
1. 그러면, A가 Normal이므로, Triangular Matrix T도 Normal이다.
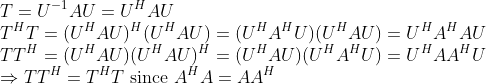
2. 그런데, Normal인 Triangular Matrix는 항상 Diagonal이어야 한다.
예시를 하나 생각해보자.
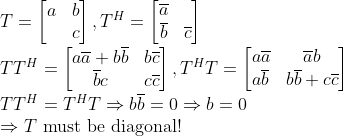
차원을 올려도 위에서처럼 Diagonal 성분에
대각성분이 아닌 것들의 Norm이 더해진 것 = 대각성분이 아닌 것들의 Norm이 더해지지 않은 것
으로 식이 계속 나오므로, 결국 모든 차원에 대해서 Normal한 Triangular Matrix T는 항상 Diagonal이어야 한다.
T가 Diagonal이라는 말은 Schur's Lemma의 결과와 합치면
T가 Eigenvalue Matrix가 되어버린다는 말과 동일하고, U는 Unitary Eigenvector Matrix로 나온다는 것을 말한다!
결국 Hermitian에서 보았던것과 같이, Normal Matrix에서도 항상 Diagonalization이 가능하다는 것을 말한다!
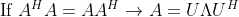
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 14-2. Quadratic Form과 극값 판별 (0) | 2023.08.28 |
|---|---|
| (선형대수학) 14-1. Definition of Positive Definite Matrix (0) | 2023.08.17 |
| (선형대수학) 13-1. Similarity Transformation, Change of Basis (0) | 2023.08.03 |
| (선형대수학) 12-2. Eigenvalue Problem of Complex Matrix (0) | 2023.08.02 |
| (선형대수학) 12-1. Complex Matrices (복소수 행렬) (0) | 2023.08.02 |



