이번시간에는 Singular Value Decompostion에 대해서 알아보자.
먼저, 우리가 지금까지 계속 해왔던 Diagonalization(혹은 Jordan Form)은 모두 정사각행렬에 대해서만 적용이 되었다.
이를 확장해서 임의의 모양을 가진 행렬에 대해서도 적용을 시킬 수 있을까???
그 전에 알아두면 좋은 Lemma를 소개하고 넘어간다.
(Lemma 1)
만일 A가 정사각행렬이고, Diagonalization이 가능한 경우, 0이 아닌 eigenvalue의 개수가 A의 rank와 동일하다!
즉, 0인 eigenvalue의 개수가 Null Space의 Dimension과 일치한다!
(증명)
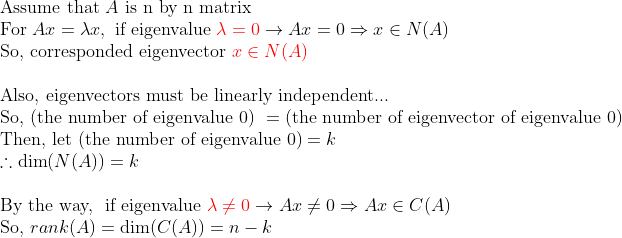
간단히 설명하자면, eigenvalue가 0인 경우에는 => 거기에 해당되는 eigenvector가 Null Space에 속한다.
게다가 eigenvector들은 모두 linearly independent이기 때문에 결국
=> 0인 Eigenvalue의 개수 = Dimension of N(A) =k
그러므로 dim(N(A))+dim(C(A))=n -> dim(C(A))=n-k=rank(A)가 된다.
이는 결국 0이 아닌 eigenvalue의 개수와 동일하다!
(Lemma 2)

(A가 정사각행렬일 필요는 없다!)
(증명)
먼저,

는 8-1에서 증명했다!
그러므로

가 성립한다.
또한, 다음은 아주 자명하다.

다음과 같은 Subspace의 orthogonality 성질을 이용하자!

그러면

이와 비슷하게 A^T에 대해서도 같은 방법으로 진행하면

인것도 동일하게 증명할 수 있다.
(Lemma 3)
A^TA와 AA^T에서 0이 아닌 eigenvalue는 동일하다. 다른 건 오직 0인 eigenvalue의 개수이다.
(증명)
Eigenvalue Problem을 살펴보면 바로 알 수 있다.
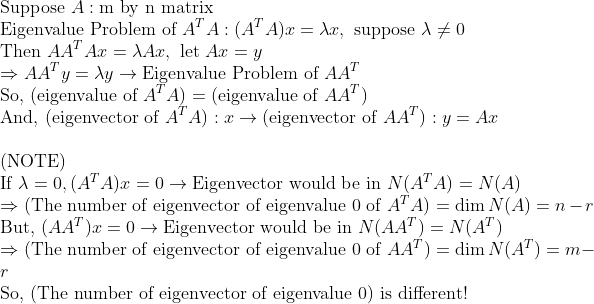
이제부터 Singular Value Decomposition이 무엇인지 살펴보자!
(Singular Value Decomposition(SVD))
모든 실수 행렬 A(정사각행렬일 필요가 없음)은 다음과 같이 Decomposition을 할 수 있다.

이 때,

Sigma가 Diagonal이라는 말은, Sigma가 (정사각행렬이 아니어도) 대각성분만 가진다는 것을 말한다.
만일, 복소수 행렬이라면, Transpose 대신 Hermitian을 쓰면 되고, Orthogonal 대신 Unitary를 쓰면 된다.
진짜로 모든 행렬이 이렇게 분해가 되는지 증명해보자.
(증명)
Orthogonal(혹은 Unitary) Matrix U, V는 각각 AA^T, A^TA가 Symmetric이라는 점을 이용해서 Eigenvalue Problem을 통해 구할 수 있으므로, 그냥 주어졌다고 생각할 수 있다.
이 때, U는 m by m, V는 n by n 행렬로 주어진다.
그러면, 우리가 보일 것은

에서, X가 정사각행렬이 아니어도 대각성분만 가지는지 확인하면 된다.
이 때, 다음과 같이 A^TA, AA^T의 eigenvalue problem을 풀어보자.
1. A^TA인 경우

2. AA^T인 경우

문제는 여기서 Sigma, Sigma'의 모양이 각각 다르다는 것이다. 이를 통일하기 위해서 다음과 같이 생각하자.
Lemma 3에 따라서 Sigma, Sigma'는 각각에 들어있는 0의 개수만 다르고 나머지는 모두 같다!
Eigenvalue가 비슷하다는 점을 이용해서 Sigma, Sigma'를 조금 더 확장해보자.
(a) m<n인 경우
A^TA에서 index가 m보다 큰 sigma들은 모두 0이 될 것이다!
그러므로, Sigma를 Sigma''로 확장시킬 수 있다.

(b) m>n인 경우
AA^T에서 index가 n보다 큰 sigma들은 모두 0이 될 것이다!
그러므로, Sigma를 다음처럼 확장시킬 수 있다.

(a),(b)를 통해서 결국 Sigma''로 위에서 AA^T, A^TA에서 쓴 Sigma, Sigma'를 대체할 수 있다!
다시 문제로 돌아오면

위의 케이스와 비교해보면 X에 Sigma''가 들어가면 딱이다!!
이 때, Sigma''는 항상 대각성분만 가지므로, X 또한 대각성분만 가지도록 만들 수 있다.
=> 그러므로 SVD는 항상 가능하다!
복소수행렬이라면 Transpose대신에 Hermitian을 넣자. 그러면, 위의 내용 그대로 따라오면, 각 성질이 문제될 것 없이 그대로 성립하므로 이 경우에도 SVD가 가능하다!
ex 1)

실제로 계산해보면

ex 2)

다음시간에 SVD의 성질에 대해서 조금 더 설명하도록 한다!
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 부록 1. 자세표현 -> SO(n), SU(n) (0) | 2023.09.10 |
|---|---|
| (선형대수학) 15-2. Singular Value Decomposition을 이용해보자! (1) | 2023.08.31 |
| (선형대수학) 14-3. Principal Axis Theorem, Sylvester's Law of Inertia (1) | 2023.08.29 |
| (선형대수학) 14-2. Quadratic Form과 극값 판별 (0) | 2023.08.28 |
| (선형대수학) 14-1. Definition of Positive Definite Matrix (0) | 2023.08.17 |



