1. Diagonalization과의 관계
Singular Value Decomposition가 "정사각행렬이 아닌 행렬"의 Diagonalization과 비슷하다는 것은 저번시간의 내용을 통해 충분히 알 수 있을 것이다.
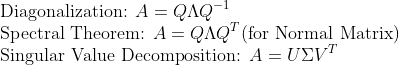
Diagonalization은 Eigenvalue Problem과 관계가 있었다.
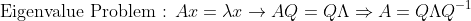
그러면 역으로 SVD는 어떤식과 관련이 있을까??
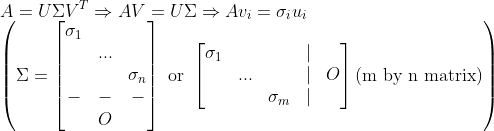
즉, 다음 문제와 관련이 있음을 알 수 있다!!
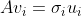
2. Eigenvalue와 Singular Value와의 관계
지난 시간의 증명을 보면, A의 Singular Value와 A^TA(혹은 AA^T)의 Eigenvalue와의 관계는 다음과 같다.
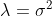
이것을 보면, Singular Value는 양수와 음수 => 둘 다 가져버릴 수 있다!
그러므로, A를 Decomposition을 하는 방법은 하나가 아니다!!!
그러나, 일반적으로 Singular Value는 양수로 잡기로 약속한다. 그러므로, SVD에 나오는 Singular Value Matrix는 유일하다고 할 수 있다.
3. Subspace와의 관계
rank(A)=r이라고 하자. 그러면, 지난 시간의 Lemma 1, Lemma 2를 이용하면
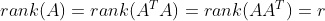
인 것과
0이 아닌 Eigenvalue의 개수가 각각 r개 있다는 것을 알 수 있다.
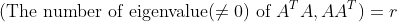
그러면, 각각의 Eigenvalue Problem을 생각해보면
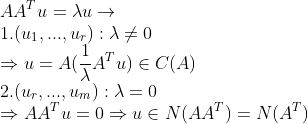
그러므로 U의 r개의 Column은 A의 Column Space에, 나머지 m-r개의 column은 A의 Left-Null Space에 존재한다.
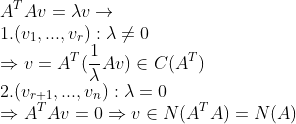
또한 V의 r개의 Column은 A의 Row Space에, 나머지 n-r개의 column은 A의 Null Space에 존재한다.
4. Ax=b를 풀어보자!
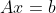
먼저, 8-1에서 보았던 Least Square Method는 A가 위아래로 길쭉한 경우(m>n)에만 적용을 했었다.
그리고, 4-2에서 보았던 일반해와 특수해를 이용하는 것은 A가 좌우로 길쭉한 경우(m<n)에만 적용을 했었다.
그러면, 이 두가지 케이스를 한번에 해결할 수는 없을까???
SVD를 이용하면 이러한 문제를 해결할 수 있다!!!
그 전에, 문제를 다시 정의해보자!
1. 위아래로 길쭉한 경우
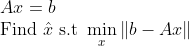
=> 이 경우에는 정확한 해가 존재하지 않을 수 있다!!
=> x_hat을 이용해서, b-Ax의 크기를 가장 줄이는 x를 찾자!
2. 좌우로 길쭉한 경우
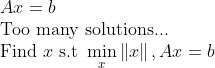
=> 이 경우에는 해가 여러가지 나온다...
=> 해 중에서 어느 것을 우리의 Optimal 해로 정할지 결정해야 한다!
=> 여기서 우리는 가장 Norm이 작은 해를 Optimal 해로 결정한다!
위아래로 길쭉한 행렬(m>n)인 경우에 사용했었던 Least Square Method에 SVD를 이용하면 어떻게 되는지 살펴보자.
먼저, Least Square Method에 대해서 다시 한번 살펴보면...
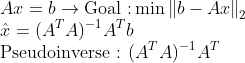
그러면 A에 SVD를 적용시켜서 어떻게 변화하는지 살펴보자.
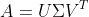
이 때, Sigma는 다음과 같이 생겼다.
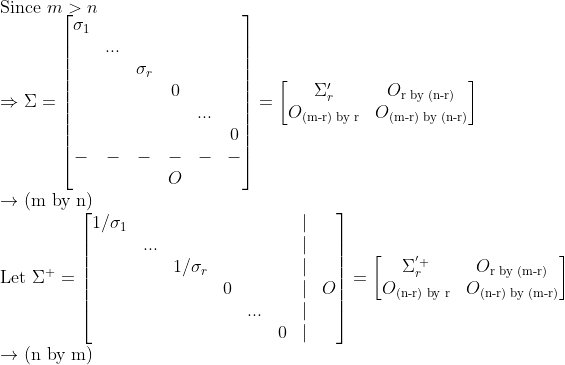
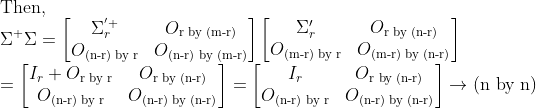
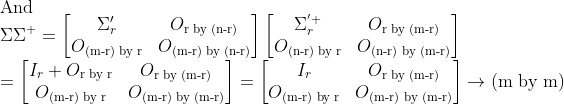
그러면, PseudoInverse는 다음과 같이 정의할 수 있다.
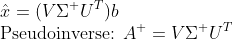
왜냐하면
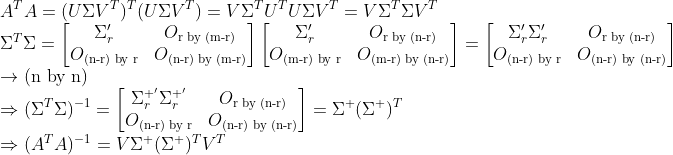
이기 때문에, Pseudoinverse를 구하면
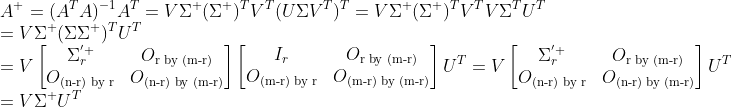
(NOTE)
이렇게 구한 x_hat은 당연히 Ax=b를 만족하지 못한다!
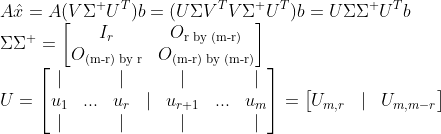
그러면,
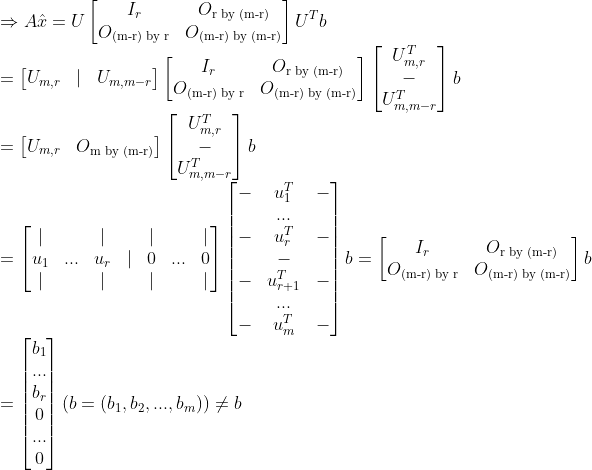
이 때, r<m이므로 결과값에 항상 0이 나오게 된다!!!
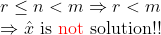
그러므로, x_hat은 절대 Solution이 될 수 없다!
이번에는 좌우로 길쭉한 경우를 살펴보자.
모든 일반해는 Homogeneous Solution과 Particular Solution으로 나눌 수 있을 것이다.
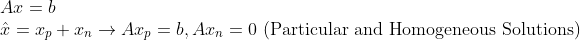
그런데, Row Space와 Null Space는 서로 수직이므로, 저 일반해를 Row Space에 속한것과 Null Space에 속한 것으로 쪼갤 수 있다.
=> 그러므로 Particular Solution은 Row Space, Homogeneous Solution은 Null Space에 속해있어야 한다!!
그러면,
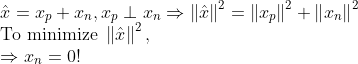
그러면 결국 가장 Norm이 작은 x_p를 구하는 문제로 귀결된다!
그러면, 여기서 SVD를 이용해보자!
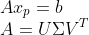
여기서 Sigma는 위아래로 길쭉한 경우와 모양이 다르다!!
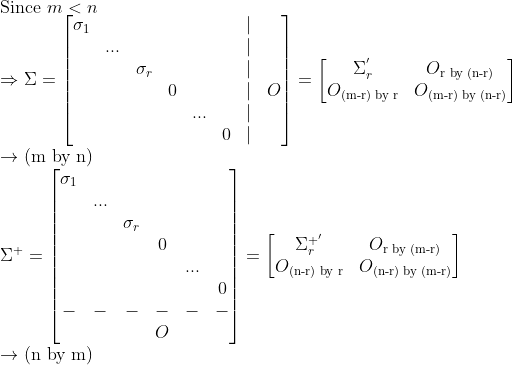
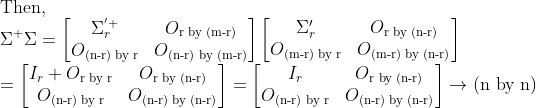
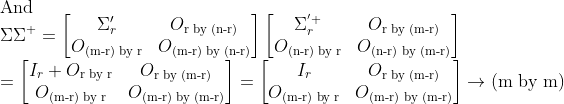
그럼 이 경우에도 Least Square Method를 통하여 x_p를 구할 수 있다. (좌우로 길쭉해도!!!)
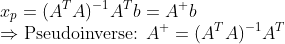
위아래로 길쭉한 경우처럼 똑같이 논리를 전개해 나가보면, 위아래로 길쭉한 경우와 행렬의 모양이 계속 같은 것을 알 수 있다.
(이는 직접 확인해보자! -> 위아래 길쭉한 경우와 똑같다!!!) 그러므로 SVD를 이용하여 Pseudoinverse를 구하면 같은 것이 나온다!
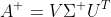
다만, 이 경우에는 이 x_p가 실제 해가 될 수 있다!!
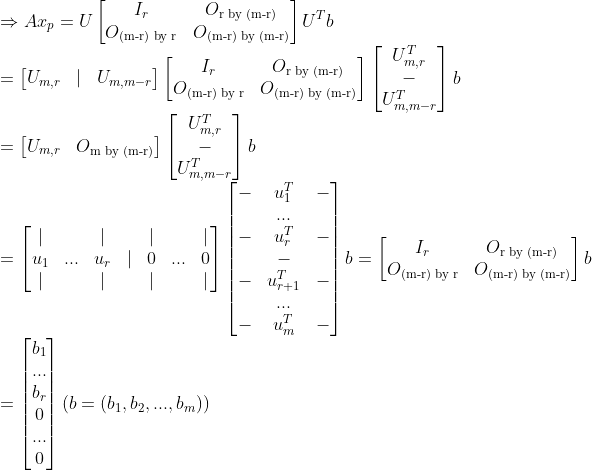
다만 이 경우에는 다음 관계가 성립한다.
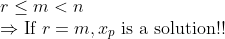
즉, Full-rank인 경우, 결과값에 0이 등장하지 않기 때문에, x_p가 Solution이 된다!!!
그리고 하나 더 알아내야 하는것이 이렇게 Pseudoinverse로 구한 x_p가 특수해 중에서 가장 Norm이 작은지 판단해야 한다.
즉, Least Square Method로 구한 저 x_p가 Row Space에 속하는지 확인하면 된다!
(만일 아니라면, Null Space에 속한 성분값이 있다는 말이므로, 길이가 최소가 아니다.)
=> 억지로 SVD를 이용해서 A^T를 만들어내면 된다!
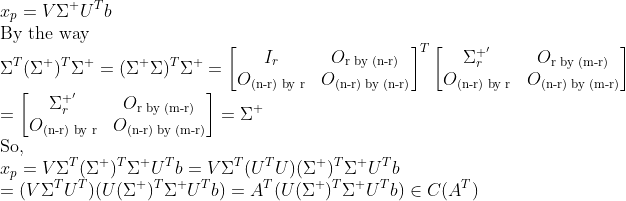
그러므로 x_p는 Row Space에 속하므로 "최소길이"의 Solution이 된다.
즉 정리하면,
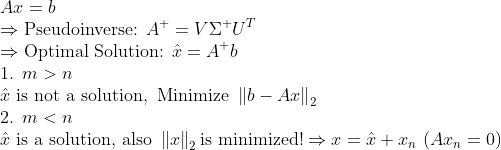
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 16. Matrix Norm(행렬 Norm) (1) | 2023.10.29 |
|---|---|
| (선형대수학) 부록 1. 자세표현 -> SO(n), SU(n) (0) | 2023.09.10 |
| (선형대수학) 15-1. Intro. of Singular Value Decomposition (0) | 2023.08.30 |
| (선형대수학) 14-3. Principal Axis Theorem, Sylvester's Law of Inertia (1) | 2023.08.29 |
| (선형대수학) 14-2. Quadratic Form과 극값 판별 (0) | 2023.08.28 |



