이번시간에는 Matrix의 Norm에 대해서 알아보자.
선형대수학에서 벡터의 Norm을 정의(7-1 참고!!)했던 것을 참고 바란다.
행렬에서도 벡터에서와 같게 Norm을 "집합의 원소의 크기를 유니크하게 결정짓는 것!"이라고 생각하는 게 좋다.
물론 선형대수학에서는 대부분 편의상 L2-norm을 사용하지만, 여러 Norm이 있다는 것을 꼭 인지하고 가야 한다!!!
먼저, 벡터 Norm을 살펴보자!
(Vector Norm)
1. Lp-norm => L1-norm, L2-norm.....

그래서, 자주 사용하는 Norm은
1-1. L1-norm

1-2. L2-norm
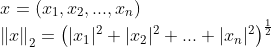
1-3. L-infinity norm
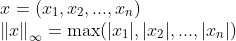
그러면, 여기서 행렬의 norm으로 확장해보자!!
일단, 우리가 아는 것은 벡터의 Norm 정의이므로, 이를 이용하도록 행렬을 벡터로 바꾸어보자!

그러면, 행렬의 Norm을 다음처럼 생각해보면 논리에 맞을 것이다!

그런데, x에 따라서 저 값은 바뀔수도 있을 것이다... 그래서 행렬의 Norm은 다음과 같이 정의한다!
(Matrix Norm)

위와 같은 정의를 따른다면 x에 상관없이, 길이의 성질을 만족하면서 행렬 A의 Norm을 정의할 수 있을 것이다!!!
(Note. 만일 행렬이 무한차원이라면, maximum 대신 supremum으로 치환될 수 있다.)
혹은 다음과 같이 표현할 수도 있다.

왜냐하면, 첫번째 정의에서 x의 상수배는 무시할 수 있기 때문이다.
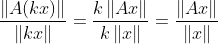
특히, 선형대수학에서는 L2-norm을 대부분 이용한다고 하였으므로, 벡터와 마찬가지로, Notation이 없다면 L2-norm이라고 생각한다.
+ Frobenius norm이라는 것도 존재하는데, 이건 아래 내용을 참고해보자!
행렬 성분별로 쪼개서 각 Norm이 어떠한 성질이 있는지 한번 살펴보자.
1. L1-norm

그런데, 이렇게 써놓으니 16-1에서 써놓은 문제와 비교해볼 수 있다!!

특히 여기서 조건으로 들어온 x의 l1-norm=1 은, 그냥 유클리드 공간에서 보면 다면체 껍데기일 뿐이다!
그러므로, 다면체의 꼭짓점에서 J는 최대/최소를 갖는다!
즉, 다음처럼 정리할 수 있다.

즉, Column Sum(절댓값) 중 최댓값이 행렬의 L1-norm이 된다!
2. L-infinity norm
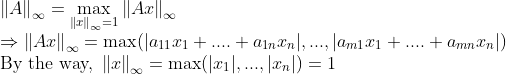
위와 같은 방식으로 생각해보면

이번에도 Condition은 다면체 껍데기가 되므로 이번에도 같은 방식으로 생각해본다면...
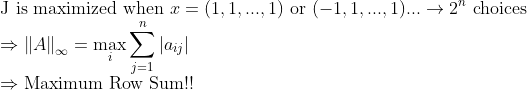
3. L2-norm
L1, L-infinity의 경우에는 약간의 Topology 배경지식이 필요해서 그냥 쓰윽 보고 지나갔을 수도 있지만, L2-norm은 Eigenvalue만 안다면 속 시원히 풀린다!!

그러므로, 그냥 심플하게 Eigenvalue로 생각하면 된다!!! (물론, 복소수행렬인 경우 Hermitian을 사용하면 된다.)


일반적으로 행렬의 Norm은 다른 언급이 없다면 이 L2-norm으로 대부분 생각한다.
4. Frobenius Norm
프로베니우스 Norm은 행렬 자체를 벡터로 생각했을 때 나오는 l2-norm 정의를 말한다.
벡터 l2-norm을 구할 때, 모든 성분을 제곱한 뒤 -> 모두 더하고 -> 루트를 씌운다!
그러면, 행렬도 이와 같은 방식으로, 모든 성분을 제곱한 뒤 -> 모두 더하고 -> 루트를 씌운다!
=> 이렇게 구한 Norm을 Frobenius Norm이라고 한다.

이 Frobenius Norm도 Singular Value와 관련이 되는데, 한번 살펴보자!

그러므로,

그런데 11-1을 참고해보면, Trace는 eigenvalue의 합이었다.

그러므로,

그러면 다음과 같은 식을 통해 L2-norm과 Frobenius Norm이 다르다는 사실을 알 수 있다!

특히, L2-norm과 Frobenius Norm을 혼동되어서 쓰는 경우가 많은데, 이를 꼭 구분해주는 것이 좋다.
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 부록 2-2. Linear Programming & Simplex (0) | 2023.11.05 |
|---|---|
| (선형대수학) 부록 2-1. Beginning of Optimization Problem (1) | 2023.11.05 |
| (선형대수학) 부록 1. 자세표현 -> SO(n), SU(n) (0) | 2023.09.10 |
| (선형대수학) 15-2. Singular Value Decomposition을 이용해보자! (1) | 2023.08.31 |
| (선형대수학) 15-1. Intro. of Singular Value Decomposition (0) | 2023.08.30 |



