Dual Problem으로 들어가기 전에, 한가지 더 짚고 넘어가야 할 부분이 있다.
"최적화 문제의 조건영역(Feasible Set) 그리고 Cost는 언제나 선형으로 표현이 되는가????" -> 결론은 "아니다"
사실 당연한 것이 조건과 Cost는 상황따라, 잡는 사람마다 달라질 것이다...
특히, Cost가 선형(Linear)인 경우 Linear Programming(LP)이라고 하고, 만일 Quadratic Form이면 Quadratic Programming(QP)이라고 한다.
그러나, 우리는 "선형"대수학 카테고리에서 최적화 문제를 보는 것이므로 Feasible Set과 Cost가 "선형"으로 표현되는 것에만 국한할 것이다.
(NOTE)
Quadratic Form의 경우 "미분"이 가능한 영역에서 Lagrangian Multiplier(라그랑주 승수법)을 이용해서 최적화 문제를 풀 수 있다!!! (https://0418cshyun.tistory.com/161 -> LQR Controller 참고)
(NOTE)
Feasible set의 경우에는 거의 대부분 "선형"으로 표현된 영역인 경우가 많다.
만일 Feasible set이 선형이 아닌 경우 거의 모든 케이스에서 어떻게든 선형으로 바꾸려고 한다. 왜냐면, Feasible set이 선형이 아니면 문제를 풀기 상당히 어려워지기 때문이다.... 이 문제는 뒤에서 잠시 살펴본다.
그러므로 우리가 다룰 최적화 문제(LP)는 다음과 같이 표현할 수 있다.

1. Minimize? Maximize? => 이 문제는 Dual Problem에서 보겠지만, 결국 최소화 문제와 최대화 문제는 동일하다.
2. cost J=cx -> 선형!
3. 조건식의 부등호 방향?? -> 어떤 방향이든 상관 없다!
4. 벡터의 부등호??? -> 각 성분마다 부등식이 있다고 생각하면 된다!
5. Dx=e??? -> 조건에는 등식도 추가될 수 있다!! -> Lagrange Multiplier 등을 이용할 수 있을 것이다.
ex)
16-1의 문제 상황을 위와 같은 꼴로 표현해보자.
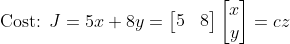


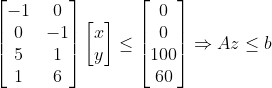
(부등호 방향 안 맞으면 마이너스 붙여서 바꾸면 된다.)
=> 그러므로 정리하면...
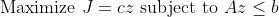
우리는 이미 예시로 저 Condition의 영역(Feasible set)이 어떻게 생겼는지 보았다!!
그런데, 더 나아가서 "일반적(즉, Feasible set이 선형)"인 경우에는 어떻게 생겼는지도 생각해볼 수 있다...
1. Az<=b
각 Row를 살펴보자...
=> 각 Row는 x가 n차원이면 다음처럼 생겼다.

부등호 말고 등호로 바꾼다면

인데, 이는 결국 n차원 공간에서 (n-1)차원 초평면(hyperplane)이 된다.
(*초평면이란?? -> 2차원 평면에서는 1차원 직선, 3차원 공간에서는 2차원 평면... => n차원에서 (n-1)차원 공간을 말함)
그런데, 이 "초평면"은 n차원 공간을 두 개로 쪼갠다.
(그냥 3차원 공간으로 생각해보면, 2차원 평면 하나는 공간을 2개로 쪼개버린다.)
그러므로

의 경우, 부등호가 달려있기 때문에
이 영역이 말하는 공간은 위에서 쪼개진 공간 중 하나를 말한다. => 당연히 Convex set이기도 하다!
그러면, Az<=b가 표현하는 영역은 위의 공간들이 "유한개" 겹쳐진(Intersection) 공간일 것이다.
(만일, 두 공간이 만나지 않는다면 그냥 empty set일 것이다.)
Convex set 유한개를 교집합하면 그 교집합도 convex set이 되므로 Az<=b로 표현된 공간은 Convex set이 되고
경계면은 Az=b인데, 이는 결국 "유한개" 겹쳐진(Intersection) 공간의 경계면 -> 유한개의 초평면으로 이루어져 있다!!!!
=> 즉, 볼록한 "다면체"로 나온다!!
(NOTE)
즉, "별 모양"은 절대 나오지 않는다는 것이다!!!
쉽게 생각하면, 저 영역 Az<=b가 표현하는 것은 2차원에서는 "볼록다각형", 3차원에서도 "볼록한 다면체"를 말한다. 단, 무한대로 쭉 뻗어나갈 수는 있다. (ex. 2차원에서 1사분면처럼 나올 수도 있다.)
2. Dx=e
=> Dx=e도 초평면 혹은 그 아래차원의 공간(즉, 3차원 공간에서 평면이나 직선)으로 해석할 수 있으므로, Dx=e를 만족하면서 Ax<=b도 만족하는 부분으로 생각하면 된다. (ex. 유한한 길이를 가진 선분을 Ax<=b, Dx=e의 조합으로 쓸 수 있다!)
그러므로 우리는 "조건"이 만족하는 영역을 "볼록한 다면체"로 생각하면 된다. (다만, 무한대로 뻗어나갈 수 있다.)
이렇게 생긴 영역을 Simplex라고 한다.
이를 토대로 16-1에서 보았었던, 극점이 영역의 Boundary에 있다는 사실을 다시 한번 증명해보자!!
특히, Linear Programming에서 극점은 영역의 꼭짓점(다면체 꼭짓점)에 있거나, 혹은 없다!

(증명)
일단, J를 미분하면 당연히 c=0인 경우 빼고, 0이 되는 경우가 없으므로, 미분으로는 증명이 안된다.
1. Ax<=b가 Bounded인 경우
Cost에 대해서 다음과 같이 생각하고,
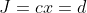
d를 변화시켜보자.

이므로, 위에서 본 것 같이 초평면!
=> 또한, Normal Vector가 c이므로, 이 초평면이 c 방향으로 움직임에 따라서 c는 그대로 있고, d만이 변화할 것이다.
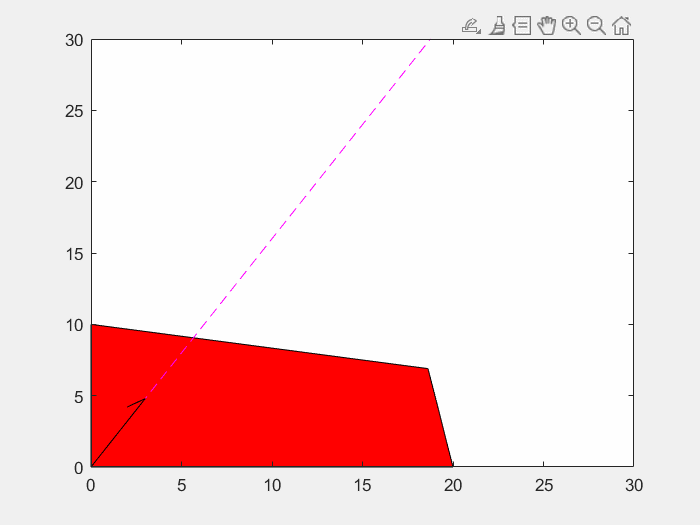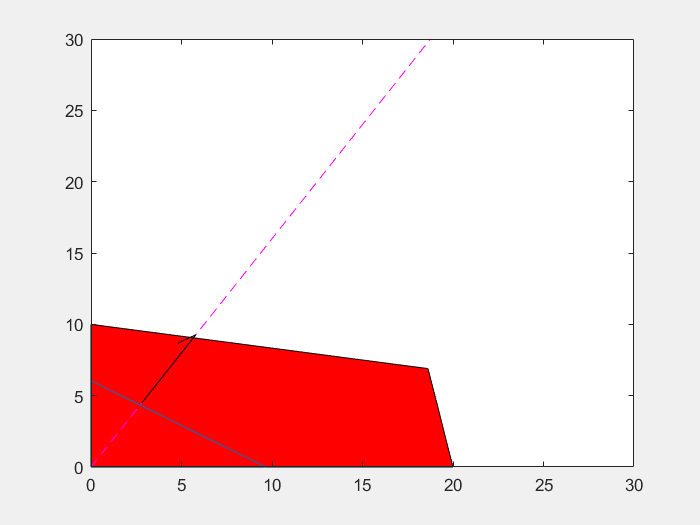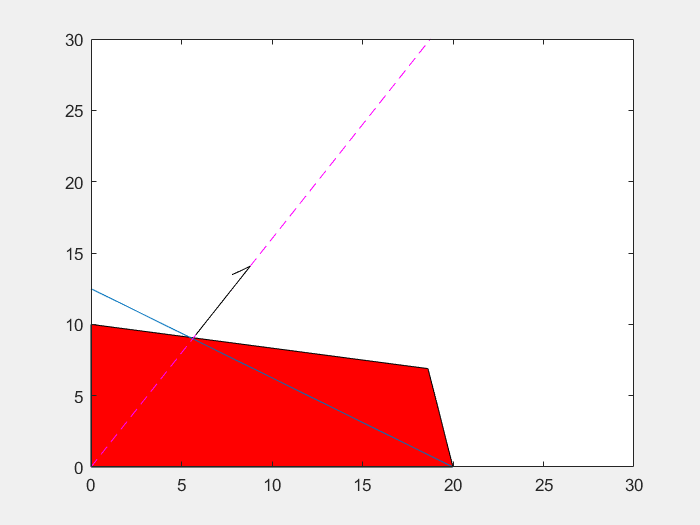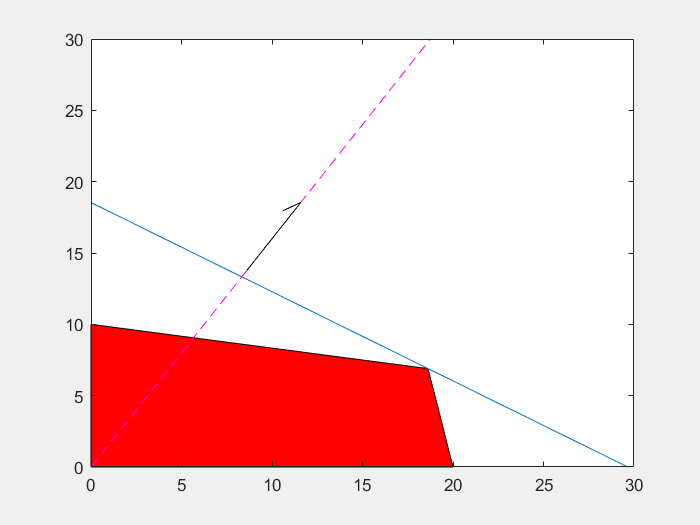
즉, Ax<=b의 각 Row가 c와 평행하지 않다면, d가 감소(혹은 증가)하다보면 결국 Simplex의 꼭짓점에 걸릴 것이고, 이 때 J가 최소(혹은 최대)가 된다. (만일, c와 평행하면, 경계면 전체에서 같은 Cost가 나올 수 있다.)
2. Unbounded인 경우
만일 d가 감소하는 방향으로 Simplex가 Bounded가 되면 1번 케이스와 동일하지만, Unbounded라면, 무한대로 d가 증가/감소하므로 극점이 존재하지 않는다!
(NOTE)
만일 J가 Quadratic Form(+Linear Form)이라면...?

1. 일단 미분이 가능하다!
=> 극점이 영역 안에 있는지 확인하고, 최소/최대를 구별한다!
2. 극점이 영역 밖에 있다면...? => 영역 안에서 J가 미분방향으로 Monotonically 증가 혹은 감소한다!
2-1. Simplex가 Bounded -> 미분방향으로 계속 움직이다보면 결국 Simplex의 경계에 걸리게 되고, 거기가 바로 우리가 원하는 최대/최소를 갖는 점이다!
2-2. Simplex가 Unbounded -> Simplex의 경계에 걸리면 그 점이 최대/최소, 만일 경계에 걸리지 않는 방향으로 움직여버리면, 최대/최소를 갖는 점이 없다!
다만, 이 때에는 미분 값이 각 점에 따라서 다르기 때문에 증가/감소하는 방향이 각 점마다 다르다!!! -> 그러나, Quadratic form의 경우, 미분 값을 계산해보면
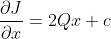
이 때, Q가 Positive(혹은 Negative) Semidefinite이면, 모든 Eigenvalue의 부호가 같아지므로, 저 미분값의 흐름이 한방향으로 몰리게 된다.
Case 1. Q=diag([2,5]), c=[1 1]

=> 왼쪽 하단, 오른쪽 상단으로 미분 방향이 몰린다!
Case 2. Q=diag([2,-5]), c=[1 1]

=> 미분 방향으로 돌리면, 회전을 한다...
그런데, 대부분의 경우 저 Q는 항상 Positive Semidefinite로 잡기 때문에(ex. LQR Controller) Case 2 같은 경우는 고려하지 않아도 된다.... (물론, Q가 Positive(Negative) Semidefintie가 아니면 문제가 복잡해진다...)
그러므로 결론을 내자면 Q가 Positive Semidefinite라면, 이번에도 최대/최소를 가지는 점은 Simplex의 꼭짓점에 존재하거나 아예 없다!
Quadratic Form에서의 설명을 봤을 때, 만약 Feasible set까지 선형으로 표현이 안된다면 -> 미분값이 한 방향으로 흐른다고 해도, Feasible set의 Boundary에 걸리는 부분이 여러 개가 나올수도 있으므로, 문제가 상당히 어려워진다..... (굳이 더 일반적으로 말하자면, Stochastic Gradient Descent를 썼을 때, 초깃값을 잘 잡아야 하는 문제로 넘어가게 된다.)
여기까지의 내용을 정리하자면...
1. Ax<=b는 "볼록한 다면체"로 생각할 수 있다.
2. Linear Programming, Quadratic Programming(단, Q의 eigenvalue 부호가 모두 하나로 일치)인 경우 미분 방향이 한방향으로 흐르기 때문에, Feasible set의 꼭짓점(경계점)에 최대/최솟값을 가지는 부분이 생긴다.
다음 시간에는 Dual Problem에 대해서 진행해본다.
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 부록 2-4. Dual Problem (0) | 2023.11.05 |
|---|---|
| (선형대수학) 부록 2-3. Example of Dual Problem (1) | 2023.11.05 |
| (선형대수학) 부록 2-1. Beginning of Optimization Problem (1) | 2023.11.05 |
| (선형대수학) 16. Matrix Norm(행렬 Norm) (1) | 2023.10.29 |
| (선형대수학) 부록 1. 자세표현 -> SO(n), SU(n) (0) | 2023.09.10 |



