(참고링크)
(미적분학) 부록1. 끝난게 끝난게 아닌 최대/최솟값 찾기 (Lagrange Multiplier): https://0418cshyun.tistory.com/40
(미적분학) 부록1. 끝난게 끝난게 아닌 최대/최솟값 찾기 (Lagrange Multiplier)
다변수함수의 미분 파트에서, 주어진 f(x)의 최댓값과 최솟값을 찾는 방법에 대해서 알아보았다. -> 이를 그냥 뭉뚱그려서 최적화 문제(Optimization)로 볼 수 있다. gradient와 hessian을 이용한 방법은 x
0418cshyun.tistory.com
저번시간에 이어서 이번에는 Lagrange Multiplier를 이용한 LQR Controller 유도를 살펴보자.
2. Lagrange Multiplier 이용
우리가 풀 최적화 문제는...
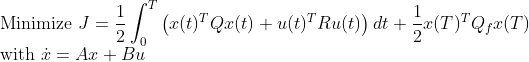
그러면, Lagrange Multiplier는...

이렇게 Lagrange Multiplier를 "확장시켜서" 사용할 수 있다.
그러면...

이 3가지 경우를 찾으면 된다!
1. u에 관한 식 => u를 구할 수 있다!

2. x에 관한 식 => lambda에 관한 식!
그러나, t=T인 경우와 t<T인 경우를 구분해야 한다!

lambda에 대한 미분방정식이 튀어나오는데, 이 Lambda를 결정하기 위해선, Boundary value이던, Initial Condition이던 필요하다. 이를 위해선 t=T인 경우를 잠시 살펴보면 된다.

나머지 x(t)인 경우를 모두 상수취급할 수 있으므로 깔끔하게 떨어진다.
=> 즉, 정리하면

이 식을 Co-State Equation이라고도 한다.
3. lambda에 관한 식 => 결국에 그냥 조건...

이 때, 1,2,3번 식을 동시에 작성해보면...

깔끔하게 1차 행렬 미분방정식으로 떨어진다.
그런데, 이미 앞에서 DP문제로 풀었을 때 우리는 u=-Kx에서 K를 알고 있다. 결국 lambda는 다음과 같이 나올 것이다.

이렇게 놓은 Lambda가 식을 만족하는지 확인하려면...
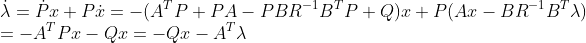
그러므로 접근을 다음과 같이 해야한다.
=> lambda를 저 Px 꼴로 놓으니 => 위의 식을 만족함 => x, lambda를 구했다!!!(물론, 이미 알고 있지만)
=> 그러나, 해의 유일성은 모른다!!!
(상미분방정식의 해를 찾을 때에도 이런 느낌의 증명을 한다! -> 일단 해를 구하고, 유일성은 그 다음에!!)
어쨌거나 정리하자면 이 경우에도
Ricatti Equation을 만족하는 P에 대해서 =>

가 "Cost"를 Minimize한다!
더 나아가서 역으로
위에서 본 Hamiltonian 미분방정식을 푼다면, Ricatti Equation도 풀 수 있다는 말이 된다.
1. Differential Ricatti Equation

이 때, Boundary Condition은 다음과 같이 잡아버릴 수 있다...

설명을 조금 더 자세히 하자면...
이번에도 Y=ZX인 Z를 잡았다고 치자... 그러면

(NOTE)
역행렬의 미분은 다음과 같이 설명할 수 있다.

그러므로, 저 Hamiltonian에서 튀어나온 Z는 Differential Ricatti Equation을 만족한다!!
=> 다음 챕터에서 나오는 Differential Ricatti Equation을 푸는 Solver도 이 방법을 이용했다.
2. Algebraic Ricatti Equation
이번에는 Algebraic Ricatti Equation을 만족하는 Z가 존재한다고 하고, Hamiltonian의 Eigenvalue들을 한번 살펴보도록하자...
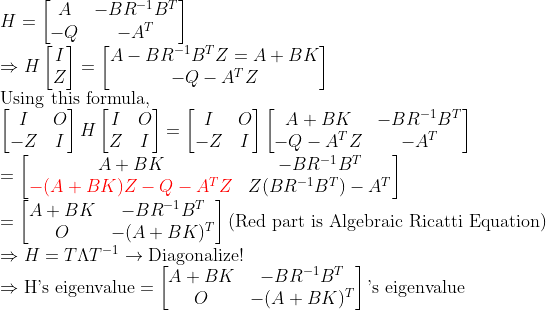
이 때, K는 LQR Controller라고 생각할 수 있고, 그러므로 A+BK는 Closed Loop System을 이야기 한다.
그런데, Block Matrix를 생각한다면 결국

일 것이다...
=> 즉, 저 Z가 존재하려면, Steady-State여야하고, 이는 결국 Stable한 Closed-Loop System을 말하기 때문에
=> (A+BK)의 Eigenvalue들은 모두 LHP에 존재하여야 한다!!
=> 반대로 -(A+BK)^T의 Eigenvalue들은 모두 RHP에 존재하여야 한다!!
결국, H의 Eigenvalue는 반은 LHP에 있고, 반은 RHP에 있다.
(A+BK)의 Eigenvalue와 eigenvector들을 알기 위해서 (A+BK)를 Diagonalize한 뒤에, 위의 내용과 종합해보자...
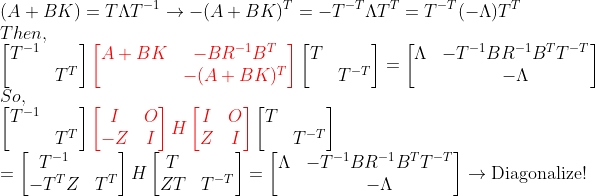
즉, 우리가 H를 Diagonalize했다!!
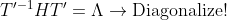
그러면, 이를 이용해서 우리가 역으로 Z를 추정할 수 있다.

=> 여기서 [T ZT]는 H의 Eigenvector들 중 일부!
=> 잘 생각해보면, 결국 eigenvalue들 중, LHP에 있는 것들에 대응되는 Eigenvector들이 바로 [T ZT]이다!
(반은 LHP, 반은 RHP에 있기 때문에, Eigenvector를 모아놓으면 반쪽짜리 홀쭉한 Matrix가 된다! => [T ZT])
그러면, Z를 구하기 위해선
=> LHP에 있는 H의 Eigenvalue에 해당되는 Eigenvector들만 골라서 [T ZT]로 놓고, 이를 반으로 쪼갠다!! => [X Y]
=> 그러면, Z=YX^{-1}!!!!
위의 내용을 거꾸로 정리해보면...
1. H를 Diagonalize하면 => Eigenvalue(반은 LHP, 반은 RHP)와 거기에 대응되는 Eigenvector(T'의 Column들)을 구할 수 있다.
2. LHP에 있는 Eigenvalue들에 해당하는 Eigenvector들을 모아놓고, 이를 반으로 자른다. -> [X,Y]
3. 그러면, Z=YX^{-1}
풀어서 설명하니 길어지는데, 실제로 구해보면 어렵지 않다!
=> Algebraic Ricatti Equation을 만족하는 Z를 쉽게 구할 수 있다!
의외로 lqr에 대한 내용이 짧게 끝나서, 추가로 몇가지 더 설명하고 끝낸다.
1. 왜 그냥 J를 미분하지 않는가??
아마 위 식을 따라오면서 이 생각이 들었을 것 같다...
LTI에서처럼

를 Cost의 x에 집어넣어서 잘 계산하면 안되나??? 라는 생각이 들 수도 있는데,
가장 문제는 뭐냐면
=> 이 문제는 LTI 시스템이 아니다!!!!
=> 즉, A,B가 t에 관한 함수이기 때문에, 미분하는 것도 문제가 생겨버린다!!

2. Infinitely Time으로 그냥 문제를 끌고 가면...?
(a) Lagrange Multiplier로 생각해보면...
=> 식이 다 나오기는 하는데, lambda에 대한 Boundary Condition을 구할 수가 없다...
=> 결론적으로 위의 내용을 이어나가기 위해서는...
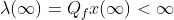
즉, x가 Bounded 되어 있어야 한다. 또한, Lambda도 Steady해야 한다!!
=> (A,B)가 Controllable해야 시간을 무한대로 늘려버릴 수 있다!
=> 결과적으로 나오는 식은 Algebraic Ricatti Equation!
(b) Dynamic Programming으로 생각할 때에도
=> V_t가 항상 Finite해야 하기 때문에, 이 경우에도
=> (A,B)가 Controllable해야 시간을 무한대로 늘려버릴 수 있다!
=> 결과적으로 나오는 식은 Algebraic Ricatti Equation!
'제어이론 > Advanced' 카테고리의 다른 글
| (Advanced) 2. 직접 LQR Controller 확인해보자! (1) | 2023.07.01 |
|---|---|
| (Advanced) 1-1. Continuous LQR Controller (Dynamic Programming 접근방법) (0) | 2023.06.30 |

