(Advanced) 2. 직접 LQR Controller 확인해보자!

(참고링크)

https://github.com/cshnforever/ricatti

GitHub - cshnforever/ricatti: Differential Ricatti Equation, Algebraic Ricatti Equation by Hamiltonian

 

---

위에서 Python 코드로 직접 Differential Ricatti Equation과 Algebraic Ricatti Equation을 푸는 Solver를 올려 놓았으니 참고바란다. -> LQR Controller까지 계산해준다.

 

다음과 같은 예시를 하나 들어보자....

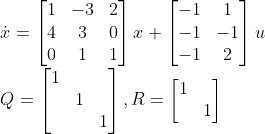
이 경우에서의 LQR Controller를 계산해보면...

 

1. Differential Ricatti Equation을 이용하면 -> 

이 때는, 각 Time Step마다, Controller K가 달라지기 때문에, 각 성분별로 값이 어떻게 변하는지만 살펴본다.

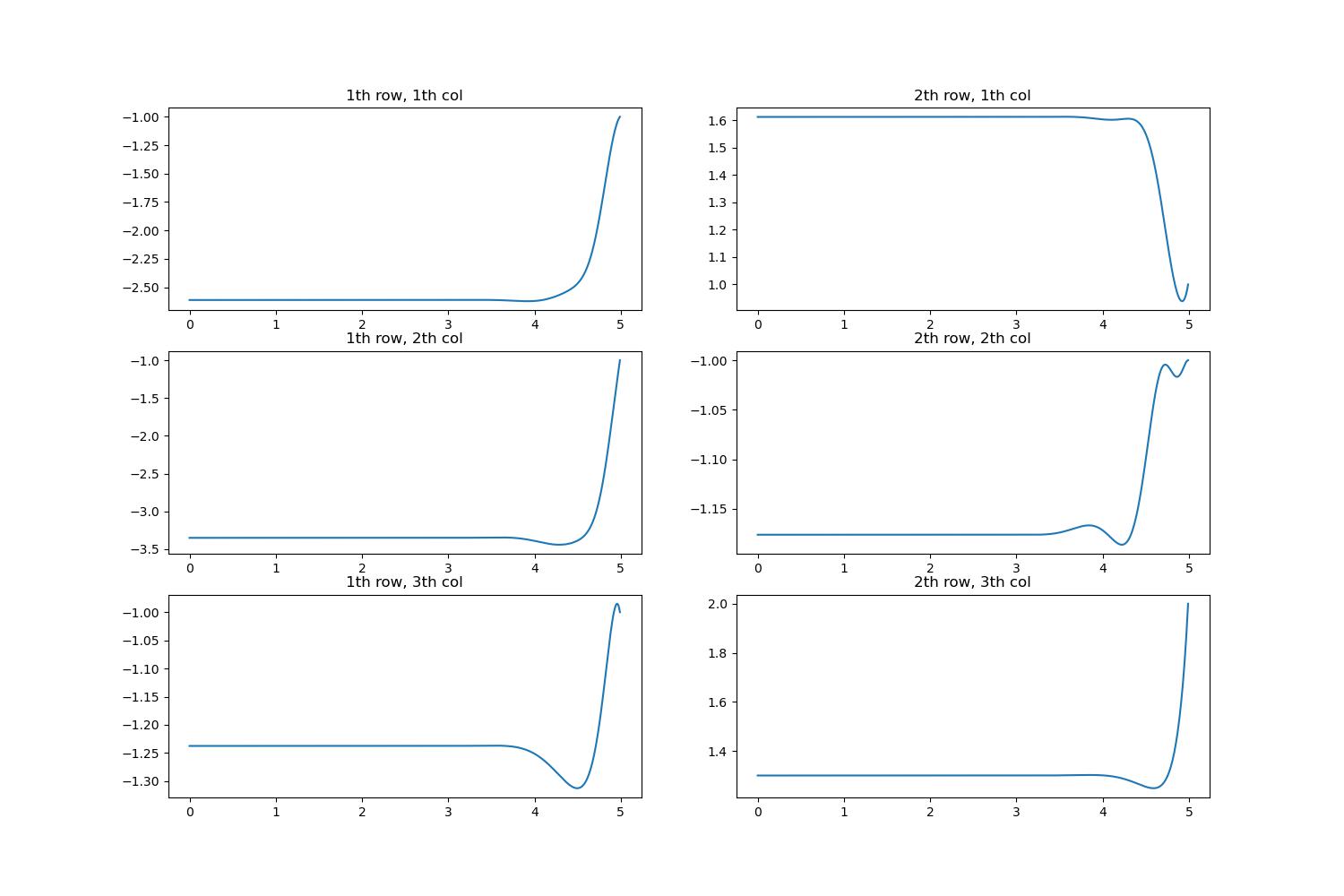
아래의 Algebraic경우와 위의 "Steady-State"에서의 값을 비교해보자... 거의 동일하다!

 

2. Algebraic Ricatti Equation을 이용하면 ->

이 때는, P가 일정하므로 LQR Controller K는...

정도로 값이 나오고,

Differential Ricatti Equation과 Algebraic Ricatti Equation을 비교해보면

다음처럼 모든 Variable이 0으로 가주는 것(Regulating)을 확인할 수 있다.

(여기서, 가려서 안보이지만 빨간선은 => Differential Ricatti Equation을 이용한 결과, 파란선은 => Algebraic Ricatti Equation을 이용한 결과)

 

---

그리고, 저 Q, R을 잡을 때....

=> 대부분 "Diagonal"형태로 잡는다! => Cost에서 Q,R의 의미를 생각해보자

=> 각 State에 대응되는 성분들이 클수록 => 더 변수의 변화를 꽉잡아줄 것이다...

ex) 위의 예시에서 

이렇게만 바꿔보자

위의 예시와 스케일이 동일해서 헷갈릴수도 있지만, 수치를 보자면...

=> 첫번째 Variable이 더 금방 0에 가까워진다 => 더 꽉 잡힘!

그러나,

=> Input의 요동침이 더 커진 것을 확인할 수 있다!

(첫번째 Input : 7 -> 8, 두번째 input: 1 -> 1.5까지 튐)

 

이와 마찬가지로 R도 동일한 방식으로 생각할 수 있다!!

(대응되는 성분이 클수록 Input의 요동침을 더 잡아준다!!)