보다 정확한 내용은 추후 "최적화문제" 카테고리에서 다룰 예정입니다!
지난 시간에는 예시를 들어서 Dual Problem을 설명했다면, 이번에는 약간 이론적으로 접근해보자. (라그랑주 승수법 혹은 KKT Condition에 대한 내용: https://0418cshyun.tistory.com/40)
이번에는 "일반적인 Nonlinear Case"부터 출발한다.
<<<Nonlinear Case>>>
먼저, Primal Problem이 다음처럼 주어져 있다고 하자.
(Primal Problem)

그러면, 이 문제에 대한 Lagrangian은 다음처럼 정의할 수 있다.
(Lagrangian of Primal Problem)

라그랑주 승수법에서 보았던 것처럼, 저 lambda와 nu는 추가로 더해진 변수이다. 이를 Dual Variables(혹은 lagrangian multiplier)라고 부른다.
즉, Dual Problem은 Primal Problem의 변수인 x가 없고, Dual variables로만 이루어진 문제를 말한다!
그러면, 이를 Dual Problem으로 치환하기 위해서 x를 없애보자. -> x에 대해서 Infimum을 취한다!
(Dual Problem)

이 때, 영역 D는 Primal Problem에서 x가 존재하는 Domain을 말한다.
그러면, g는 다음 부등식을 만족한다.
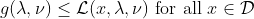
그런데 Primal Problem(최소화 문제)에서 cost를 최소화하는 것은 이 Lagrangian을 최소화하는 것과 동일한 문제이므로

그러므로, Primal Problem의 해가 존재한다면, Dual Problem에서 g도 항상 위로 유계이다.
(Weak Duality)
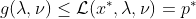
여기서 만일 g의 최댓값이 저 p*가 된다면 => g는 Primal Problem과 대응되는 Dual Problem이다!!
(즉, g의 Optimal Cost(최댓값)이 Primal Problem의 Optimal Cost(최솟값)과 동일하다!)
하지만, 저 g의 최댓값이 존재하는지조차 불분명하고, 이를 해결하기 위해서 최댓값 대신 Supremum 값으로 그냥 끌어온다고 할지라도 g의 최댓값이 p*가 된다는 보장도 사실은 없다. (Dual의 최댓값과 Primal의 최솟값의 차이를 Duality Gap이라고 한다.)
그러나, 조건 영역이 Convex set, Cost가 Convex function인 Convex Optimization에서는 저 g의 최댓값이 존재하고, p*라는 사실이 보장된다!!! => 이를 (Strong Duality)라고 한다!
그리고 저 lambda와 nu가 어떤 영역에서 존재하는지 살펴보기 위해 다시 Lagrangian을 끌어와보자.

결국 Primal Problem -> 최소화 문제에서 cost를 최소화하는 것은 이 Lagrangian을 최소화하는 것과 동일한 문제이다.
그런데, lambda에 관해서....
f_i(x)<=0이므로, Lagrangian을 더 줄이기 위해서 lambda들은 굳이 0보다 작을 필요가 없다!!!!
그러므로 lambda와 nu 영역의 조건을 다음과 같이 생각할 수 있다.

그러므로, Dual Problem에서 Optimal Cost를 다음과 같이 작성할 수 있다.
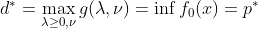
정리하자면 Dual Problem은 다음과 같다!!

<<<Linear Case>>>
이번에는 Linear Case에 대해서 생각해보자.
(Primal Problem)
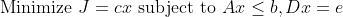
위와 같은 방식으로 Lagrangian을 정의하면 (Row로 다 풀어서 쓰면 된다!)
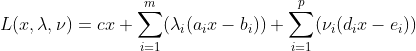
그러면 Lagrangian Dual Function은

그러면, Nonlinear Case와 완전 동일하게 생각할 수 있으므로, 자세한 설명은 위의 설명으로 대체한다.
(NOTE)
만일 부등호조건만 존재하고, x>=0 조건이 있다면 조금 더 깔끔하게 쓸 수 있다.

그러므로, 저 (-L)에 대해서 Dual Problem을 작성해보면 다음과 같다. (부등호 방향 주의)

Dual Problem을 살펴보면, 결국 "조건의 개수"가 Dual Variables의 개수라는 것을 알 수 있으므로,
만일 Primal Problem이 어렵다면, Dual Problem을 이용해서 최적화 문제를 풀어보는 것도 생각할 수 있다. (물론, 항상 Dual Problem이 쉽다는 것은 아니다!!!!)
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 부록 2-3. Example of Dual Problem (1) | 2023.11.05 |
|---|---|
| (선형대수학) 부록 2-2. Linear Programming & Simplex (0) | 2023.11.05 |
| (선형대수학) 부록 2-1. Beginning of Optimization Problem (1) | 2023.11.05 |
| (선형대수학) 16. Matrix Norm(행렬 Norm) (1) | 2023.10.29 |
| (선형대수학) 부록 1. 자세표현 -> SO(n), SU(n) (0) | 2023.09.10 |



