역행렬이 존재할 조건 (즉, 역행렬이 존재한다와 "동치"인 명제들)을 정리합니다!
여기선 "정사각행렬(n by n)"인 경우만 생각합니다. (일단 길쭉한 것들은 정확한 "역행렬"의 의미가 아니므로)
행렬 A(n by n)에 대해서 역행렬이 존재한다는 것은
1. A가 Invertible하다! (이 말 자체가 역행렬이 존재한다는 뜻입니다.)
2. A의 Columns / Rows 가 모두 Linearly Independent
3. A의 Column / Row Space의 차원(Dimension) = n
4. A의 rank -> rank(A) = n (Full-rank)
5. A의 Pivot에 0이 존재하지 않는다.
6. A의 Reduced Form (혹은 Echelon Form)에 [0,0,0,...0]으로 쭉 밀리지 않는다!
7. Ax=0의 해가 x=0 하나 밖에 없다!(해가 유일!)
8. Ax=b의 해가 x=A^(-1)b 하나 밖에 없다!(해가 유일!)
9. A의 Determinant (det(A))가 0이 아니다!
10. 모든 Eigenvalue / Singular Value가 0이 아니다!
(9, 10번은 아직 내용이 나오지 않았으므로, 설명을 패스합니다.)
1~6번까지는 앞에서 다 설명한 내용이고,
7~8번은 모를 수도 있을 것 같아서, 설명하고 넘어갑니다.
먼저, 당연히
(역행렬이 존재한다면) => (7,8이 성립!!)
은 당연합니다...
(증명)

A의 역행렬이 유일하기 때문에, 위에서 구한 x도 당연히 유일한 solution일 것입니다!
그러면, 반대로는 어떻게 증명할까요???
(7 or 8이 성립) => (역행렬이 존재!)
(증명)
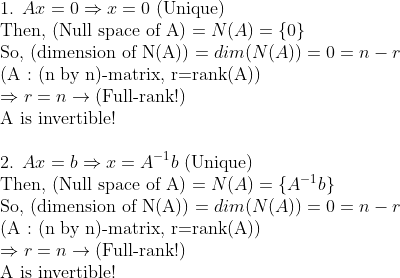
한 point는 0차원이라는 것을 사용하면 바로 증명할 수 있습니다!
자, 이를 통하면 만약에 A가 역행렬이 존재하지 않는다면...
=> 1. Ax=0의 경우, x=0이 항상 해가 되기 때문에, 그리고, Null space의 Dimension이 0보다 크기 때문에(즉, 1차원 이상)
=> 무수히 많은 해(Null space에 있는 모든 점이 해!)를 가진다!
=> 2. Ax=b의 경우, b가 C(A)에 있나 없나에 따라서, 해가 있을 수도 있고, 없을 수도 있기 때문에
=> 무수히 많은 해(Null space에 있는 모든 점이 해!)를 가진다! / 혹은, 해가 없다! (b가 C(A)에 존재하지 않는다!)
그러면, 역행렬이 존재하지 않는 조건들도 살펴봅시다.
행렬 A(n by n)에 대해서 역행렬이 존재하지 않는다는 것은
1. A가 Singular matrix! (이 말 자체가 역행렬이 존재하지 않는 matrix라는는 뜻입니다.) / non-invertible
2. A의 Columns / Rows 가 모두 Linearly Dependent
3. A의 Column / Row Space의 차원(Dimension) < n
4. A의 rank -> rank(A) < n (Not Full-rank)
5. A의 Pivot에 0이 존재한다.
6. A의 Reduced Form (혹은 Echelon Form)에 [0,0,0,...0]으로 쭉 밀린다! (이 zero-row를 가진다!)
7. Ax=0의 해가 무수히 많다!
8. Ax=b의 해가 없거나 무수히 많다!
9. A의 Determinant (det(A)) = 0
10. Eigenvalue / Singular Value에 0이 존재한다!
(9, 10번은 아직 내용이 나오지 않았으므로, 설명을 패스합니다.)
(추가)
좌우로 길쭉 / 위아래로 길쭉한 경우엔?? => 5-2 참고!
=> 차원을 높이는 쪽의 inverse는 존재하지 않음!
=> 차원을 내리는 쪽의 inverse는 그 차원만큼 Full-rank인 경우, inverse가 존재!
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 7-1. Inner Product(내적)과 Norm (0) | 2023.06.26 |
|---|---|
| (선형대수학) 6. 선형사상과 행렬 (Advanced!) (0) | 2023.06.23 |
| (선형대수학) 5-2. Rank와 역행렬(Left / Right / Two-sided Inverse) (0) | 2023.06.20 |
| (선형대수학) 5-1. 계속 나오는 Rank! -> 정의(Definition) (0) | 2023.06.20 |
| (선형대수학) 4-3. Span, Basis, Dimension (0) | 2023.06.19 |



