Frequency Domain에서의 Control은 PID Controller로
Error 자체, 기울기, 적분값에 비례해서 Controller를 만들어 주었다.
그러면, 이러한 State Variable System에선 어떤 식으로 Controller를 만들어 줄 수 있을까?
-> 8-1에서 본 것 같이, Input에 Feedback을 먹여서 Controller를 만들 수 있다!
u = -Kx
그런데, Frequency Domain에서는 Zero나 Pole의 위치로 이러한 Controller의 안정성이나 성능을 알 수 있었는데, 여기서는 어떻게 할까????
다음을 살펴보자...
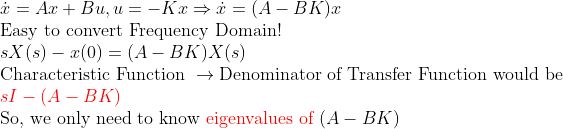
즉, 저 특성방정식이 결국 Closed-loop system의 Pole의 위치(Eigenvalue)를 말해주므로, "시스템의 안정성"을 바로 파악할 수 있을 것이다!!
->> 결국 K를 조절해서 Pole의 위치를 조절하는 방식으로 Controller를 설계할 수 있다!!
->> Pole-Placement!
(NOTE)
결국 Controllability라는 것은 State-Variable을 마음대로 움직일 수 있다는 말이므로, 결국 모든 Closed-System의 Pole의 위치를 내 마음대로 결정할 수 있다는 것과 동일하다!!
(NOTE)
이러한 K를 어떻게 잡는가? -> 아래 github에서의 코드를 살펴보자! (Gradient Descent!)
그러면 Regulation 문제를 생각해보자...
Controller를 달면, 우리의 문제는....
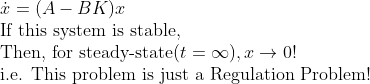
y의 경우도 결국 y=Cx+Du에서 x->0으로 가므로, y->0이라고 할 수 있다. (대부분의 경우 D=0)
그러면, Tracking 문제를 Controller를 이용해서 해결해보자.
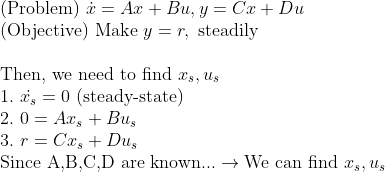
이렇게 찾은 Steady-state Variables와 steady-state Input을 가지고
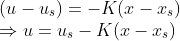
처럼 Controller를 설계하게 되면 y -> r로 움직일 것이므로, Tracking 문제를 해결할 수 있다.
Example)
(Regulation Problem)
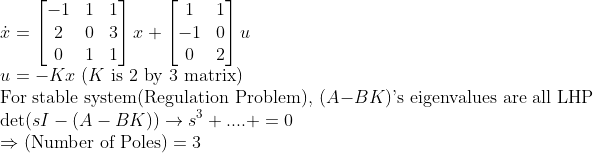
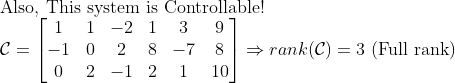
그러면, Pole 3개를 모두 원하는 위치에 놓을 수 있다!
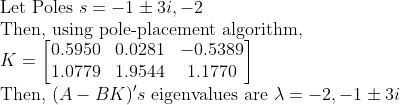
(NOTE)
이 때, K의 변수는 6개이고, Pole은 3개이지만 결국 2개(Conjugation 관계) -> 복소수이므로, Pole을 결정하는 것은 4개...
그러므로 (K의 변수) > (Pole 결정개수) -> K가 유일하지 않다!!
이 때의 Response를 살펴보면... (초깃값은 모두 1!)
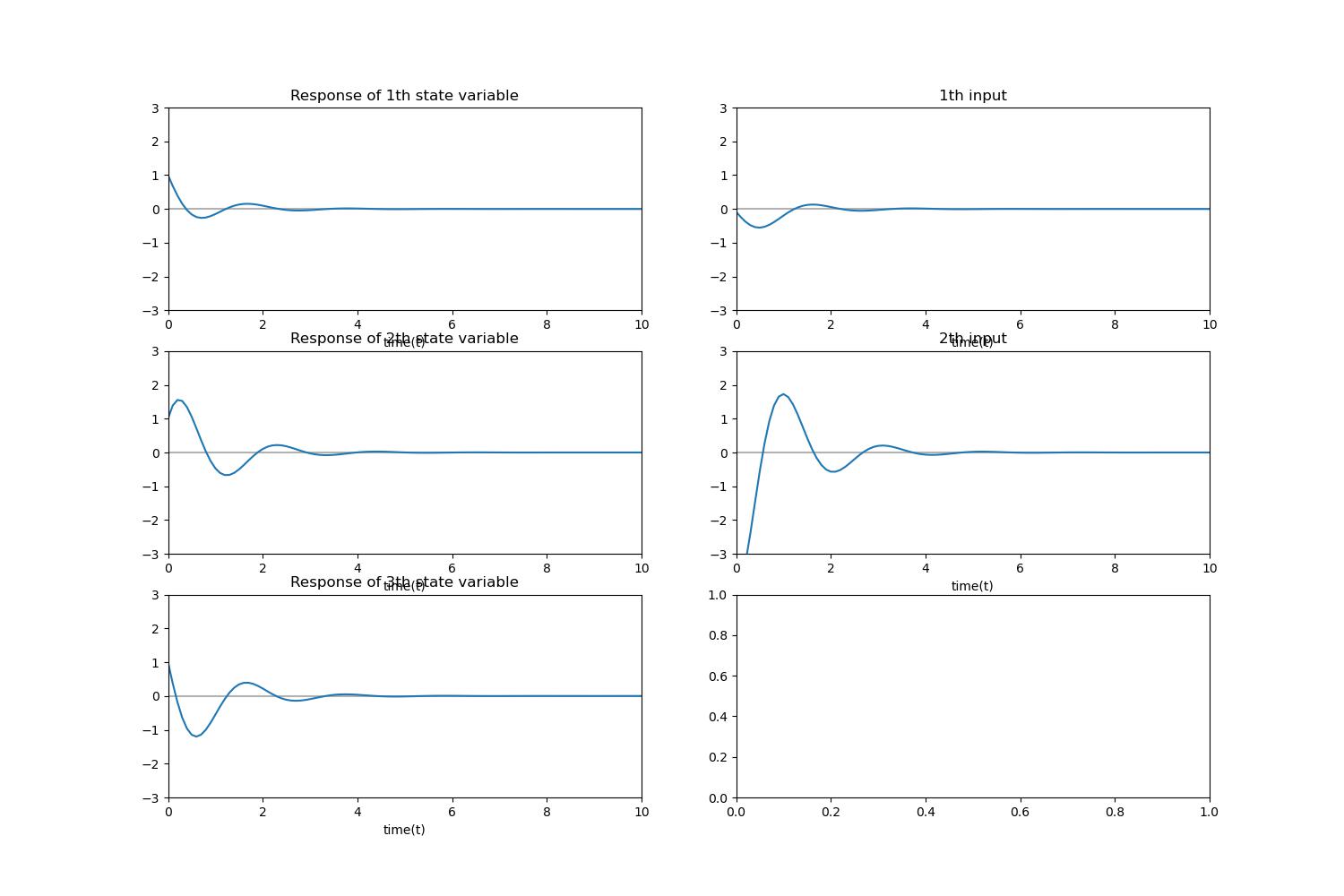
(Tracking Problem) (수정되었습니다!!!!)
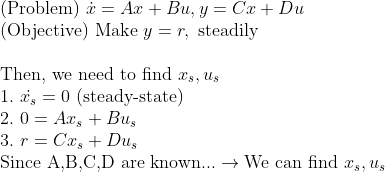
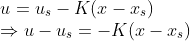
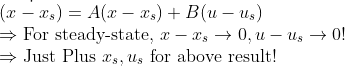
즉, 위의 x_s에 대해서, u_s를 구할 수만 있다면 Regulating Problem에서 평행이동만 한 것이다!
x -> (x-x_s), u -> (u-u_s)로 바꿔버리면 나오는 결과일 뿐이다! (평행이동일 뿐, 시스템의 안정성에 영향을 주지 않는다.)
(Example)
위의 Regulating Problem에서 각 Variable이 [-1,0,2] 를 Tracking 하도록 해보자.
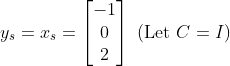
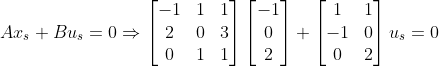
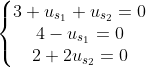
식은 3개인데, 변수는 2개이므로, u_s를 결정할 수 없다! => 결국엔 어느정도 "Trade-off"가 필요하다.
여기선 가장 심플하게 생각할 수 있는 Pseudo-Inverse를 생각해보자.
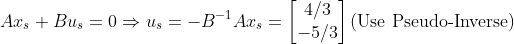
("""수정전에는 u_s의 부호가 바뀌어 있었습니다!!!!)
문제는, Pseudo-Inverse에는 오차가 있다!
위의 u_s를 가지고 다시 x_s를 구해보면...

원래 의도한 바는 위와 동일한 K를 가지고 다음과 같이 바꿔버리는 것이었는데,
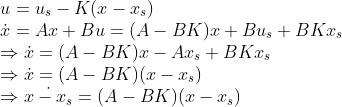
Psuedo-Inverse의 오차에 의해서 다음과 같이 바뀌어진다.
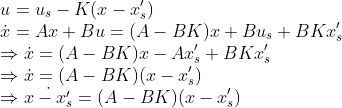
이러한 시스템의 시뮬레이션 결과를 뽑아보면 의도한 대로 가지 않는 것을 확인할 수 있다!!!

이유를 따져보면, Pseudo-Inverse로 u_s를 구하면, Ax_s+Bu_s=0이 성립하지 않으므로, " (다른 Steady-State x_s') "에 걸린다!!
(수렴성은 변하지 않는다! -> "A-BK의 Pole"이 결정하므로!!!!)
근본적인 원인을 따져보면... => 2개의 Input으로 3개의 Output을 결정하려고 하기 때문으로 볼 수 있다!!!
그러면, 이를 가장 [-1,0,2]로 잘 끌고 갈 수 있는 방법은 무엇일까...???
1. Pseudo-Inverse :

에서 오차가 있다는 말은 "Steady-State 시간"에 오차가 있다는 말로, 애초에 우리가 원하는 것과는 "다른 Steady-State"로 끌고 간다... 그러나, K에 대해선 독립적이므로, 수렴성은 보장해준다.
2. 이를 해결하기 위해서 LQR(Advanced 카테고리 참고)을 사용할 수 있다. (물론, 무조건적인 해결책은 아니다.)
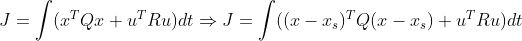
LQR은 "시간"에 따라서 오차를 조절해줄 수 있기 때문에, "Steady-State(Infinite Time)"에 대해서 오차를 최대한 줄여주도록 만들수 있다. 그러나 이렇게 수정하면서 K가 바뀌게 되므로, Regulating Problem에서는 잘 수렴하다가 Tracking Problem으로 오면 수렴이 안 되는 경우도 생길 가능성이 있다.
아래 Github에서 코드를 참고 바란다! (2023-05-23 Updated!!!)
https://github.com/cshnforever/tf
GitHub - cshnforever/tf: Transfer Function for Linear System
Transfer Function for Linear System. Contribute to cshnforever/tf development by creating an account on GitHub.
github.com
'제어이론 > 선형시스템 -> LTI System' 카테고리의 다른 글
| (선형시스템) 8-4. State Estimator(Observer) (1) | 2023.05.23 |
|---|---|
| (선형시스템) 8-2. Controllability and Observability (1) | 2023.05.18 |
| (선형시스템) 8-1. Intro. of Full-State Feedback Control (0) | 2023.05.17 |
| (선형시스템) 7-4. Lead/Lag Compensator (0) | 2023.04.25 |
| (선형시스템) 7-3. Stability in Frequency-Domain -> Nyquist Plot (1) | 2023.04.24 |



