저번 시간에는 K(그냥 Real number)를 움직이면서, closed-loop system의 안정성을 살펴보았다.
=> K의 변화를 통해 Unstable -> Stable한 시스템으로 만들어 줄 수 있다!
그런데, 그 K 자리에 (즉, Controller 자리) 그냥 실수만 들어갈 수 있는가???
그건 아니다. 그 자리에 그냥 시스템 하나만 들어가면 된다.(다만, 물리적으로 가능한 것만 -> Proper Transfer Function을 가지는 시스템)
가장 간단하게 들어갈 수 있는 것이 바로 PID Controller인데, 이번 챕터에서 살펴보자!
(PID Controller)
-> 오차(Error)에 대해서
P: Proportional -> 비례!
I: Integration -> 적분!
D: Derivative -> 기울기!
센서가 없는 경우의 Closed Loop System으로 가정해보자.

여기서 눈여겨 볼 것은 Controller로 들어가는 신호인데, 바로 Error가 된다! (E=R-Y)
1. P controller
-> 오차(Error)에 비례해서 output을 뱉는다.

-> 가장 심플한 Controller!
-> Root Locus에 바로 적용이 가능하다!
-> 그러나, plant의 특성을 Closed-loop system이 거의 다 가져가기 때문에, 그닥 좋지 않은 성능...
-> Steady-State Error를 생각한다면 K가 커야 Steady-State Error를 줄일 수 있을 것이다!!!

그러나, 이 K가 커지면 Closed-Loop System의 고유진동수 자체가 커질 우려가 있으므로, Transient Response에는 안 좋을 것이다.

2. I Controller
-> 오차의 적분값에 비례해서 Output을 뽑는다!

-> 이 경우에는 s=0에 Pole을 놓기 때문에, Steady-State Error의 관점으로 본다면 System Type이 하나 증가!!!
-> Steady-State Error를 해결할 수 있다!
-> 그러나, 에러가 쌓이려면 시간이 필요하기 때문에 Transient Response에는 역시 안 좋다...
3. D Controller
-> 오차의 미분값(기울기)에 비례해서 Output을 뽑는다!

-> 그런데, 들어가기 전에 문제가 생긴다!
-> 이 시스템은 Improper Transfer Function... -> 즉, 미래를 알아야지 지금 값을 계산할 수 있다!! => 실제할 수 없다!!
-> 그러므로, 어쩔 수 없이, "바로 지금"의 미분 값이 아니라, "한 스텝 전"의 미분 값을 쓰게 된다. (물론 미분값도 Finite하게 근사한 값을 쓰게 된다.)
-> 다만, 만일 "존재한다면", 오차의 변화(기울기)는 아주 빠르게 반영이 가능하므로, Transient Response에는 좋을 것이다!
-> But, s=0에서 Pole 하나를 없애는 것과 마찬가지이므로, Steady-State Error에는 악영향...
각각 장단점이 다르므로, 대부분 이를 합쳐서 쓰게 된다!!
-> PI, PD, PID Controller!
게다가, 여러 개를 쓰면, 복잡하긴 하지만, 자유도를 높이는 효과(PID 다 쓰면, 변수가 3개이다!)가 있어서, 주어진 성능을 맞추는데 조금 더 유리한 측면이 있다.
4. PI Controller

-> 이 경우에는 s=0에 pole을 넣었기 때문에, Steady-State Error는 해결....
-> K_p가 굳이 막 커질 필요가 없다!
-> 그냥 I Controller보단 P에 의해서 Transient Response가 낫다.
5. PD Controller

-> P Controller보단 Transient Response의 성능을 잡을 수 있겠지만, Steady-State Error는 해결하기 어렵다.... (심지어 K_p를 크게 한다고 해도, System Type이 바뀌어야 하기 때문에...)
6. PID Controller
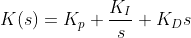
-> 복잡해지긴 하지만, 가장 Desirable하다...
-> 각 변수들을 바꿔가면서 성능을 조정할 수 있다!
예를 들어서...
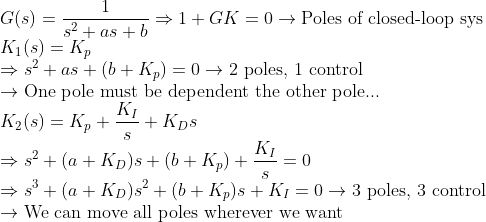
--> 맨 뒤 3개 항(2차, 1차, 0차)만 보자면
--> k_I는 진동수 관련!, k_p는 수렴에 관련!, k_d는 값 사이의 전체적인 조절을 해준다고 할 수 있을 것이다.
예시를 들어보자!!

Closed Loop -> (GK)/(1+GK)!
이 때, P Controller를 하나 설치해보자...
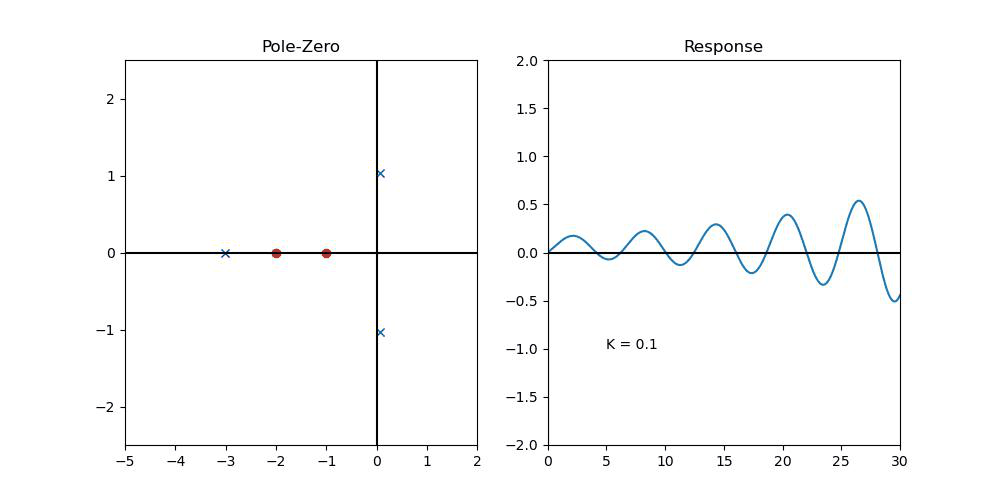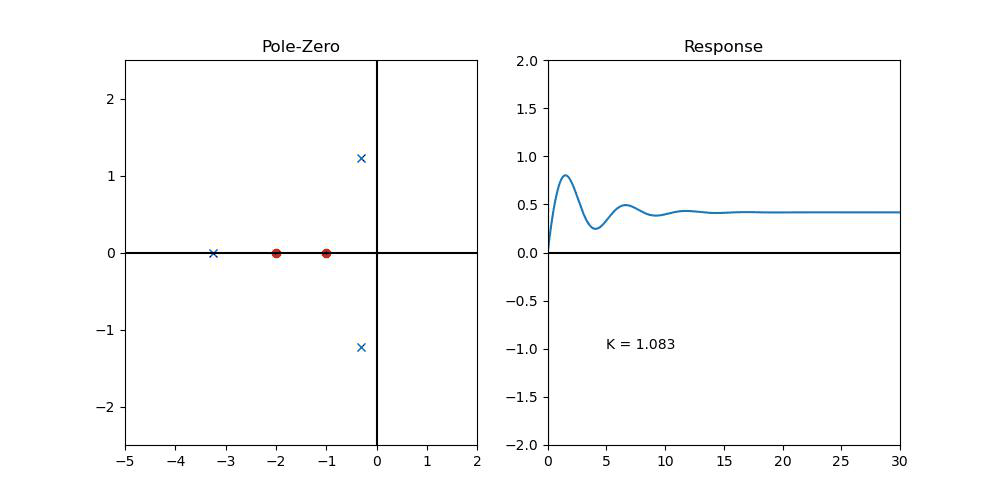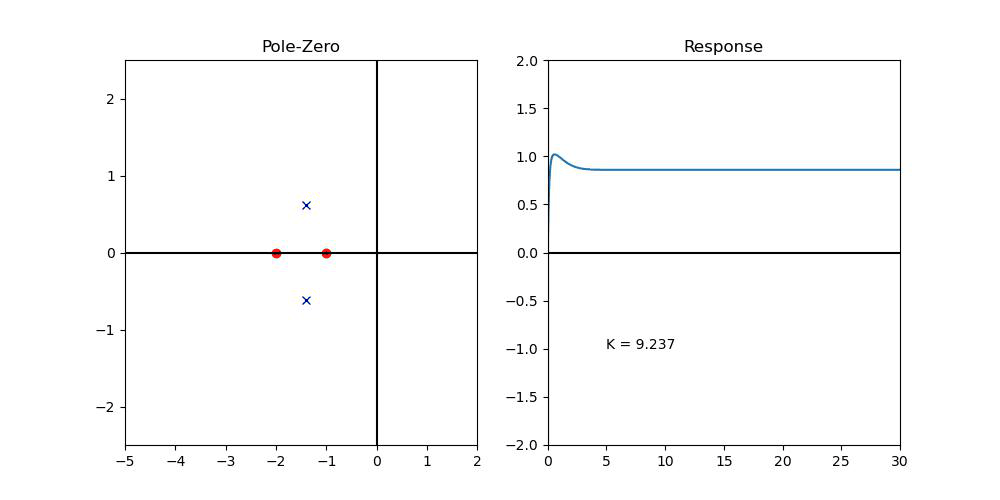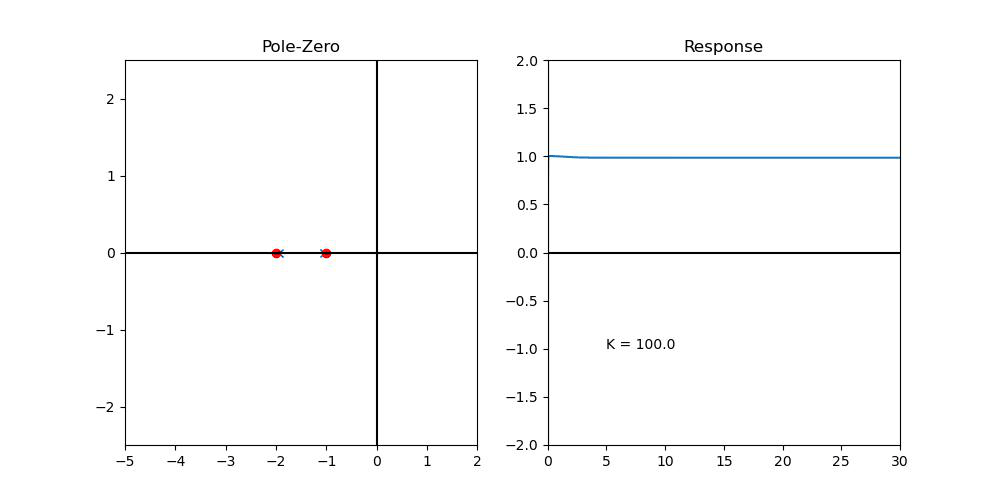
위의 Closed-Loop System의 Pole이 LHP로 끌려오는 것을 볼 수 있다!! (Like in Root-Locus)
문제는, K가 작으면, Steady-State error가 생긴다는 것을 확인할 수 있다! 그렇다고 K를 냅다 크게 할 수도 없는 것이, Input에는 분명히 한계치가 있기 때문이다!
그럼 이를 해결하기 위해서, Integral항을 넣어보자.
먼저 K_p=1이면 일단 LHP에 있으니, K_p=1이라고 하고, 계산해보자...(여기서 K는 K_I)
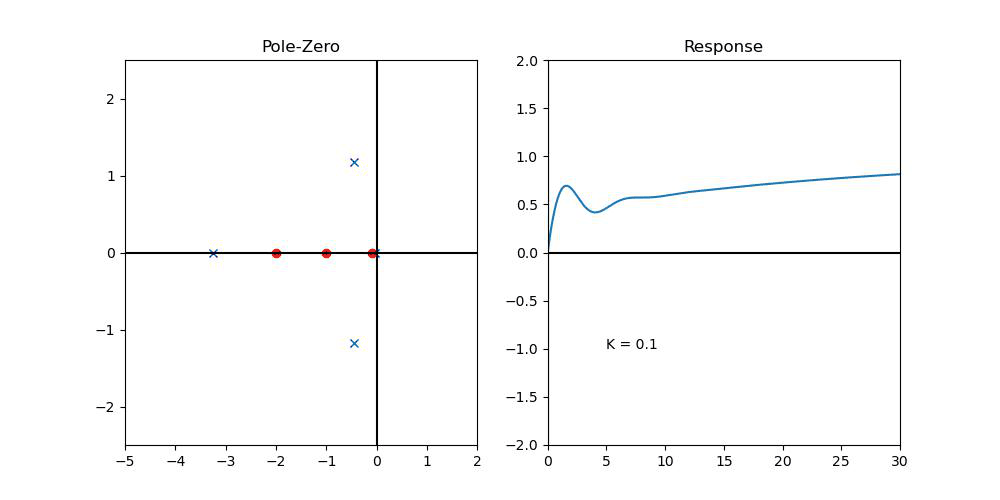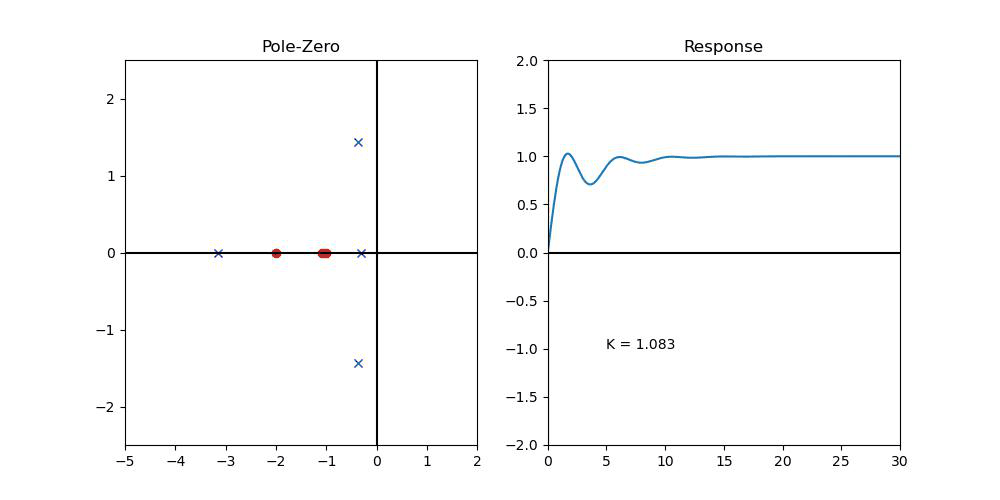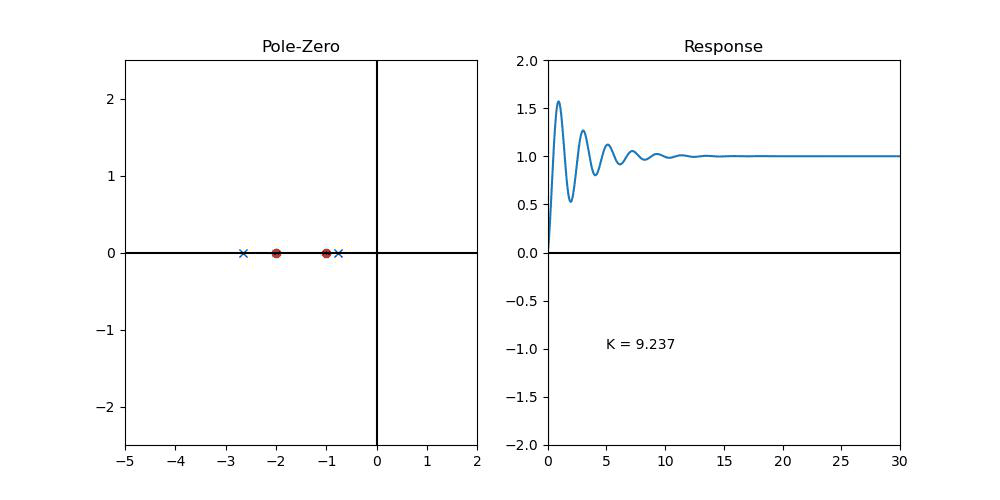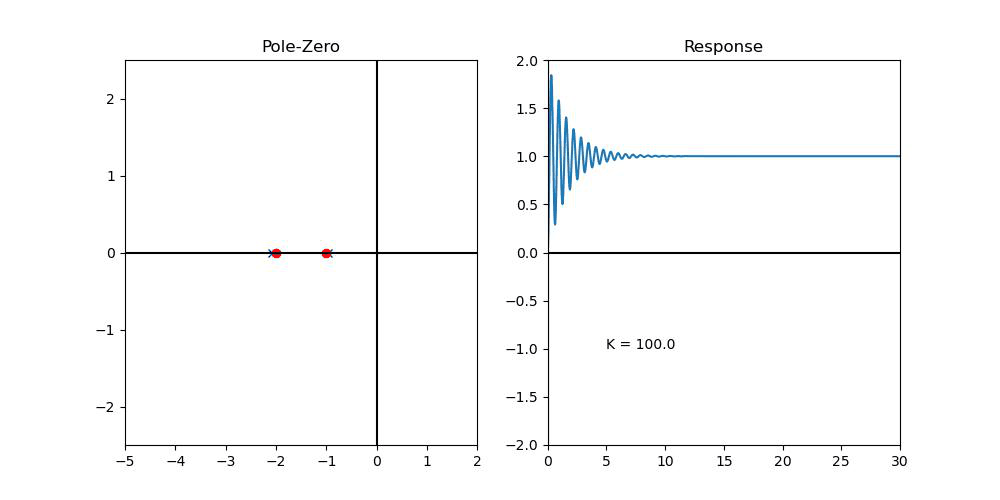
일단, Steady-State Error는 잡힌 것을 확인할 수 있다.
그러나, K_I가 커짐에 따라서 진동이 커진다는 것을 확인할 수 있을 것이다. (Complex Pole이 멀어진다....)
그러면, 이를 해결하기 위해서 PID 다 써보자! (이 경우에는 k_p=1, k_i=10이라고 가정하자, 아래에서의 k=k_d)

k_d가 늘어남에 따라서, (s의 2차항)이 늘어나면서 k_I때문에 생긴 진동부분을 상쇄해주는 것을 알 수 있다.
(위의 Closed-loop system의 Transfer Function을 보면서, 혹은 Complex Pole을 Zero가 상쇄시켜주는 것을 보면서...)
-> Transient Response에 효과적!
그러나, 너무 k_d가 크게 되면, k_I와 k_p항의 효과를 잃어버릴 수 있다
그러므로, Root Locus와 함께 Pole-Zero가 어떻게 움직이는지 잘 확인해야 좋은 Controller를 설계할 수 있을 것이다.
그런데, 위에서 말한대로, 실제로 D Controller는 Proper Transfer Function을 가지지 못하기 때문에, 문제가 있다.
그러므로, 이를 어느 정도 따라하는 Compensator로 이를 모방할 수 있다.
(Lead Compensator)
PD Controller를 모사할 수 있다!!

Zero를 0에 아주 가까이 놓는 대신에, Pole을 아주 멀리 떨어뜨려 놓는다!
(Lag Compensator)
PI Controller를 모사할 수 있다!!

Pole를 0에 아주 가까이 놓는 대신에, Zero를 아주 멀리 떨어뜨려 놓는다!
왜 이름이 Lead, Lag인지는 다음 챕터에서 알아보고, 진짜로 PI, PD Controller를 따라가는지 살펴보자...
위의 예시를 통해서 반응을 살펴보면...
1. Lead Compensator
-PD Controller
k_p=0.1, k_d=1
-Lead Compensator
Zero=-0.1, Pole=-10


2. Lag Compensator
-PI Controller
k_p=0.1, k_i=1
-Lead Compensator
Zero=-0.1, Pole=-10

물론, 각 상수를 약간씩 조정하긴 해야하지만, Lead/Lag Compensator가 PD, PI Controller의 기능을 하는 것을 알 수 있다!
+ NOTCH Compensator
Imaginary Axis에 거의 붙어있는 Pole(성능 Bad!)을 상쇄하기 위해서, 그 근처에 Zero를 붙여준다.
그러나, 이 경우에도 PD Controller와 같은 상황이 펼쳐진다....
그러므로, 이 Zero를 또 상쇄시키기 위해서 실수 축 멀리 Pole을 붙여준다!
예를 들어서...
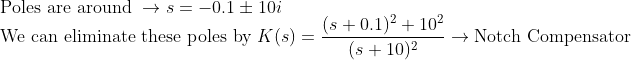
반응을 한번 보면...
위에서 PI Controller를 달았던 것이 Imaginary Axis 근처에 Pole을 가지고 있었는데,
여기에 더해서 Notch Controller를 또 추가로 달자!


이런 식으로 성능이 안 좋은 Pole을 상쇄시킬 수 있다!!
(전달함수에 관한 Python 코드)
-> Pole, Zero 계산 및 Time-Domain으로 변환해주는 코드입니다!
https://github.com/cshnforever/tf
GitHub - cshnforever/tf: Transfer Function for Linear System
Transfer Function for Linear System. Contribute to cshnforever/tf development by creating an account on GitHub.
github.com
'제어이론 > 선형시스템 -> LTI System' 카테고리의 다른 글
| (선형시스템) 7-2. 시스템이 얼마나 안정한가? (Gain Margin, Phase Margin) (0) | 2023.04.24 |
|---|---|
| (선형시스템) 7-1. Bode Plot (0) | 2023.04.21 |
| (선형시스템) 6-1. Root Locus -> 안정성 with Manipulation (0) | 2023.04.12 |
| (선형시스템) 5-3. System Type with Steady-State Error (0) | 2023.04.12 |
| (선형시스템) 5-2. 어떻게 원하는 output을 얻을 수 있을까? (Tracking, Regulation Problem) (0) | 2023.04.11 |



