(미적분학) 2-2. 음수항이 있는 급수는 어떻게 하지? (Alternating Series Test, Absolute Convergence)
(해석학 참고링크)
-교대급수, 절대수렴-
(해석학) 5-2. 시그마(급수)는 막 곱하면 안 되나??? (Convergence of Series 2): https://0418cshyun.tistory.com/55
(해석학) 5-2. 시그마(급수)는 막 곱하면 안 되나??? (Convergence of Series 2)
(미적분학 참고링크) -교대급수, 절대수렴- (미적분학) 2-2. 음수항이 있는 급수는 어떻게 하지? (Alternating Series Test, Absolute Convergence) : https://0418cshyun.tistory.com/5 (미적분학) 2-2. 음수항이 있는 급수
0418cshyun.tistory.com
앞 챕터에서 양수항을 가지는 급수만을 다루었다면 이번 챕터에서는 음수항을 가지는 급수에 대해서도 다뤄볼 것이다.
1. (Alternating Series)(교대급수)
급수의 일반항의 부호가 계속 교대로 나오는 급수 (+, - ,+ , -, +.....)
(Alternating Series Test)
다음과 같은 양수항 Sequence {a_n}에 대해서
1. 수열이 Decreasing Sequence를 만족한다.

2. 일반항이 0으로 수렴

그러면 다음과 같은 Alternating Series

은 수렴한다.
(증명)
주어진 수열이 Decreasing Sequence이므로 교대급수에서
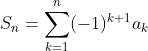
이라고 한다면
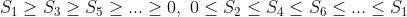
을 만족한다.
그러므로
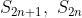
두 수열 모두 bounded, monotonic sequence이므로 둘 다 수렴한다.
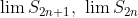
둘 다 값이 존재하므로(수렴)
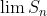
또한 값이 존재한다.(수렴)
이 Test는 앞에서 보았던 단조수열의 수렴성을 급수로 확장한 것이라고 할 수 있다.
2. (Absolutely Convergence)(절대수렴)
급수

에 대하여

가 수렴한다면 위 급수는 절대수렴한다고 한다.
(Absolutely Convergence Test)
절대 수렴하는 급수는 수렴한다.

(증명)
절댓값을 벗기기 위해 약간의 트릭을 쓴다.
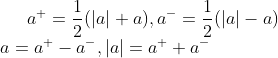
a가 양수인 경우 a+는 a, a-는 0, a가 음수인 경우는 a+는 0, a-는 -a가 된다.
이 때, comparison test를 생각해보면
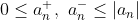
이므로 a+, a-로 이루어진 급수는 수렴한다.
그러면
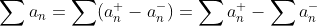
이므로 a_n으로 이루어진 급수도 수렴한다.
이번 챕터에서는 음수항을 가지는 급수에 대해서도 수렴성여부를 확인하였다.
테스트 하는 방법 자체는 꽤 직관적이지만 그걸 유도하는 방식을 하나씩 까보면 그렇게 만만하지는 않다는 걸 알 수 있다.
정확한 방법은 해석학 설명으로 넘기기로 하고 다음으로 넘어가도록 하자.
이제 우리는 이러한 급수를 이용하여 공대에서 가장 powerful한 tool인 테일러 급수에 대해서 알아볼 것이다.