(미적분학) 17-2. 드디어 마지막, 스토크스 정리 (Divergence, Curl in 3D, Stokes' Theorem)
지난 챕터에선 2차원 평면에서의 divergence와 rotation을 보았다. 이번엔 3차원 공간에서 알아보자.
정의는 2차원과 똑같다!
(Divergence(발산))

(Curl)

보면 알겠지만 rotation은 curl의 2차원 버전이었다고 생각하면 된다.
의미도 2차원과 동일하므로 생략한다. (생략한다고 중요하지 않은게 아니다!)
발산정리와 그린정리도 동일하게 성립한다. (다만, 그린정리 -> 스토크스정리)
(Divergence theorem)(2차원<->3차원)

이 때 normal vector의 방향은 앞과 같이, 밖으로 나오는 방향으로 정한다.
증명은 앞 챕터에서 했으므로 생략한다. n차원으로도 충분히 확장 가능하다.
(Stokes' Theorem)(1차원<->2차원) in 3D

그린 정리와 뭔가가 비슷하면서도 약간 다른 느낌이다. -> 다중적분이 아니라 면적분으로 되어 있다.

윗 그림을 예로 들면 boundary는 빨간 선, D는 뚜껑없는 구면을 생각하면 된다.
그러니, 결국 curl이 rotation이라는 것을 생각하면, 그냥 그린정리를 3차원에서 생각한 것에 불과하다.
(증명)
경계면을 어떻게 구하는지 주목하자.
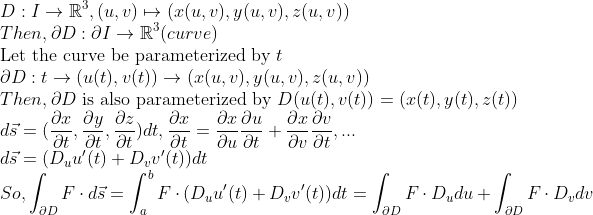
그런데,
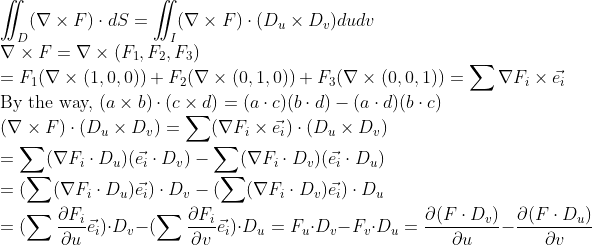
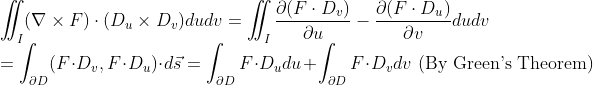
여기서 꽤나 많은 벡터 외적 성질을 이용하게 되는데, 이는 (나중에) 선형대수에서 다룰 기회가 또 있을 것이다.
Green's Thm, Stokes' Thm과 선적분에서 했던 Potential Function(잠재함수) 개념을 생각해보자.
1. (Curl and Potential Function)
만일 벡터장 F가 Potential Function을 가지면, curl F=0이다.

2. (Same boundary)
서로 다른 두 곡면이 같은 boundary를 가진다면,
(if boundary 방향 같다면)

(boundary 방향 반대이면)

3. (Closed Surface)
폐곡면에서

(폐곡면을 두 개로 쪼개서 생각하면 2번에 의해 바로 구해진다. (boundary 방향 서로 반대))
자, 여기까지가 우리가 알아본 대학교 미적분학이다.
난이도가 어땠을지는 모르지만, 뒤로 오면서 선형대수도 좀 알아야 편한 부분들이 있기 때문에 초심자에겐 다른 카테고리보다 오히려 어려울 수도 있겠다.
공부하는 팁이라면 개인적으로 문제를 풀어보면서 감을 익히는 것이 좋고, 개념적으로는 이 정도만 해도 공대에서 학부수준에서는 충분하다. (대학교 다니는 4년동안 이 개념들 잘 써먹는다.) 심지어 다른 과목들을 본다고 해도, 개념적으로는 이보다 더 들어가는 경우는 없다. 물론, 엄밀한 증명을 위해서 다른 책들을 본다면 모를까....
이 후에 나오는 부록 챕터들은, 분명 배우긴 하는 개념들이지만, 내용의 흐름상 생략한 부분들을 정리할 것이다.
자, 드디어 끝!!!!