(선형시스템) 8-2. Controllability and Observability

지난 챕터에서 잠시 언급한대로,
1. (관측하는 값) y에서 x를 모두 추정할 수 있는가??? -> Observability
2. 우리가 x(혹은 y)를 원하는 대로 움직일 수 있는가??? -> Controllability
에 대한 내용을 이번 시간에 다룰 예정이다.
먼저, Controllabiliy에 대해서 살펴보자.
문제를 좀 더 정확하게 표현하기 위해 다음과 같은 질문을 해보자.
-> x 혹은 y를 결정시키는 것은 어떤 것이 있을까??
-> 선형시스템을 그냥 미분방정식처럼 생각한다면
-> 1. 문제(위에서 A,B,C,D), 2. 초깃값(Initial Value) // (미분방정식에서 Initial Value Problem이라고 하는 바로 그것!)
이 있을 것이다.
그러면, 우리는 Controllability의 정의를 다음처럼 생각할 수 있다.
(Controllability)
임의의 초깃값 x_0(t=0)에서 유한 시간 안에 State Variable x(혹은 y)를 원하는 대로 움직일 수 있는가?
-> 임의의 초깃값 x_0(t=0)에서 유한 시간 안에 Input u를 잘 주어서 State Variable x(혹은 y)를 원하는 값으로 만들 수 있는가?
=> 즉, 어떤 초깃값이 되었든간에 Input u를 잘 주면, 유한시간 안에 x를 원하는 값으로 만들 수 있으면 Controllable하다.
ex1)

이 선형시스템의 Solution을 계산해보면...

u와 t를 잘 주면, 어떤 a1, a2든 만들 수 있고, 또한, e^{At}가 역행렬이 존재하므로, 이에 의한 Dimension 축소는 일어나지 않을 것이다. 또한, 초깃값은 결과값에 그냥 상수를 더한것일 뿐이므로, 영향을 주지 못한다.
그러므로, 어떤 x_1,x_2든 u, t만 잘 주면 만들어 낼 수 있다!
그러므로 이 시스템은 Controllable하다.
ex2)

왠지 딱 봐도 문제가 생길 것 같다...
사실, 이건 수식적으로 표현할 필요도 없는 것이...
x2는 Input에 의해서 움직일 가능성이 있지만,
x1은 input에 의해서 직접적인 영향을 받지 않고, 또한 x2에 의해서 input에 의한 간접적인도 영향을 받지 않는다.
즉, x1은 Input과는 전혀 연관이 없다!
-> 그냥 x1은 초깃값정도에만 영향을 받기 때문에, x1을 원하는 값으로 만들 수 없다!
위에서 Controllability를 확인한 방법을 조금 더 세련되 -> Observability게 써보자.
(Cayley-Hamilton 정리(케일리-해밀턴 정리))
혹시나 예~전에 행렬 수업을 들어봤다면, 기억할 수 있는 정리이다. (대부분 2 by 2이었음)
1. 2 by 2

이는 사실 그냥 행렬 수식 다 정리하면 이를 보일 수 있다!
2. Generally....
사실은, 이 정리는 Eigenvalue를 구하는 방법으로부터 나왔다. -> 즉, 모든 정사각행렬이 Characteristic Equation을 가지고 있다는 것을 뜻한다.
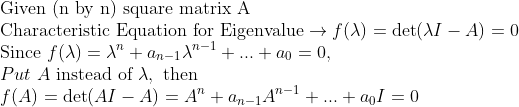
이를 활용하면,
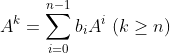
임을 알 수 있다!! -> High-order 항을 그냥 0~(n-1)차 항으로 다 낮출 수 있다!
이 Cayley-Hamilton 정리를 활용하여, Controllability를 확인하는 방법을 알아보자.
(Check for Controllability) -> Controllability Matrix

여기서 빨간 부분으로 칠해진 Matrix C를 Controllability Matrix라고 한다.
(Note) C는 n by (mn) matrix이다! (not 1 by n)
그러므로 여기서 C가 Full-rank이어야야 x(t)를 원하는 데로 놓을 수 있다고 말할 수 있다!!! -> ex1을 확인해보자!
(추가 Note)
위에서 e^(At)가 Invertible이라고 했는데 -> 사실 여기에는 한 가지 가정이 더 숨었다!
A의 Eigenvalue가 0이 되면 안된다!!!! (즉, A가 Invertible해야 한다.)
만일 A의 eigenvalue가 0이 된다면, Jordan Form이 되었든 Diagonal Form이 되었든, 한 줄이 0으로 쭉 밀리는 상황이 발생하므로, singular matrix가 된다.
사실, 이는 A의 singularity 체크로 쉽게 확인할 수 있다!
-> A가 Singular이면, A의 Eigenvalue에 0이 포함된다!!!
정리하면, 저 Controllability Matrix C의 rank(C)가 full-rank! (rank(C)=n)
여기까진, LTI 시스템에 대해서 적용할 수 있지만,
LTV시스템이 되면, A,B가 t에 의존하기 때문에, e^(At)을 논의하는데 상당히 애매해진다.... -> 이 방식을 쓰지 못한다!
LTV시스템인 경우는 Controllability Gramian이라는 것을 이용하는데, 이는 나중에 LTV 시스템을 다룰 때에 다시 언급한다.
이번에는 Observability에 대해서 살펴보자...
이번에도 문제를 좀 더 명확하게 해보자.
-> (관측하는 값) y에서 x를 모두 추정할 수 있는가???
-> "Input u는 우리가 주는 것이니 알고 있다!"

이렇게 본다면, 위에서 모르는 것은 오직 초깃값 x(t_0)이다.
=> 결국 y로부터 x를 추정한다는 말은, x의 초깃값 x(t_0)를 추정한다는 말과 동일해진다!!
(Observability)
모든 유한 시간 t에서, 주어진 y(t)로부터 state-variable x(t)를 추정할 수 있는가? (Input u(t)는 우리가 주는 것이니 알고 있다!)
=> 주어진 y(t)에서 초깃값 x(t_0)를 추정할 수 있는가???
만일 가능하다면, 이 시스템이 Observable하다고 한다.
ex1)

y만 가지고, x를 추정할 수 있는지 살펴보자...

그러므로 x를 추정할 수 있다!!(역행렬 존재)
ex2)

이번에도 같은 방식으로 해보면...

역행렬이 존재하지 않으므로, 모든 x를 추정할 수는 없다!!!
(Check for Observability) -> Observability Matrix
이번에도 Controllability와 동일한 방법으로 접근한다!
위의 y에 대한 식에서 결국 영향을 주는 것은 첫번째 항이므로, 첫째항만 가지고 생각한다.

여기서 빨간 부분으로 칠해진 Matrix O를 Observability Matrix라고 한다.
(Note) O는 (mn) by (n) matrix이다! (not n by 1)
그러므로 여기서 O가 Full-rank이어야 x(t_0)를 알 수 있다!!!
정리하면, 저 Observability Matrix O의 rank(O)가 full-rank! (rank(O)=n)
이 경우에도 마찬가지로 LTV 시스템에 적용할 때 문제가 생기므로, LTV 시스템에서는 적용할 수 없다.
선형시스템 2-2의 내용을 잠시 복기해보자...
(선형시스템) 2-2. 마음대로 잡아도 되는 State-Variable (Equivalent System of LTI): https://0418cshyun.tistory.com/120
(선형시스템) 2-2. 마음대로 잡아도 되는 State-Variable (Equivalent System of LTI)
이번에는 선형시스템에 대해서 State Variable을 마음대로 잡아도 되는 것을 보인다. -> 다만 표현에 변화가 생긴다! 일단 주어진 LTI 시스템에 대해서... 이 때, 내가 마음대로 State-Variable을 바꾸어보
0418cshyun.tistory.com
이렇게 Equivalent한 시스템에서의 Controllability와 Observability는 당연히 보존이 되어야 할 것이다!! (P가 nonsingular!)
왜냐하면, 결국 동일한 정보를 가지고 있기 때문이다.
그리고 여기서 나왔던 Controllable Form(Control Canonical Form), Observable Form에 대해서 조금 더 살펴보자...
(Controllable Form) -> Always Controllable

이 경우에서 Controllability Matrix를 구해보자...
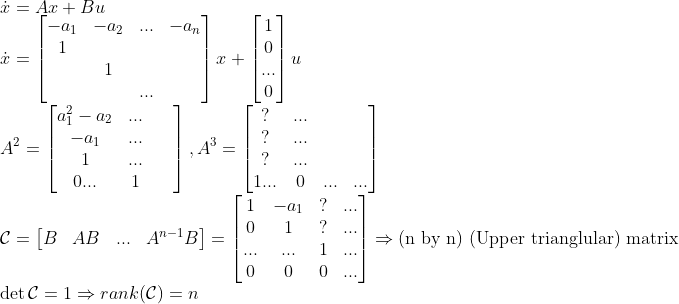
그러므로, 이렇게 변환할 수 있는 LTI 시스템은 항상 Controllable하다!!!
(Observable Form) -> Always Observable
이번에도 마찬가지 방법으로 접근한다.

단지 Controllable Form을 Transpose 시킨 것밖에 없다!!
그러므로, 이렇게 변환할 수 있는 LTI 시스템은 항상 Observable하다!!!
-> Controllable이 아니거나 Observable이 아니라면, 이러한 Form으로 변환시키는 nonsingular P가 존재하지 않는다는 것이다!!!
8-1에서 (측정값 y의 개수)와 (State Variable x의 개수)에 대해서 잠깐 언급했는데,
이를 Controllable과 Observable의 관점으로 잠시만 살펴보면...
(NOTE -> State variable은 우리가 그냥 임의적으로 잡는 것이라는 것을 생각하자!!! -> 개수도!)
1. Uncontrollable이라는 것은 -> 주어진 시스템에 Redundant State-Variables... w.r.t Given Inputs(u)
즉, 집어넣은 input의 개수에 비해서 불필요한 State Variable이 너무 많다는 것을 의미한다.
=> 즉, Input의 개수를 늘려서 시스템을 바꾸던지, 아니면 몇 가지 State Variable은 포기하던지
2. Unobservable이라는 것은 -> 주어진 시스템에 Redundant State-Variables... w.r.t Given sensor value(y)
즉, 가지고 있는 센서값으로는 주어진 State Variable이 너무 많다는 것을 의미한다.
=> 즉, 센서의 개수를 늘려서 시스템을 바꾸던지, 아니면 몇 가지 State Variable은 포기하던지
=> 그러므로, 시스템의 성질은 유지하면서, 불필요한 State-Variable을 제거하는 것이 필요하다!
=> 이렇게 최소의 State Variable 개수로 하는 System Realization을 Minimal Realization이라고 한다!!!
이에 대한 논의는 Advanced 카테고리에서 보도록 한다.
다음 챕터에서는 이를 이용한 State-Feedback Control에 대해서 간략히 설명한다.